Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 101585 by Rohit@Thakur last updated on 03/Jul/20

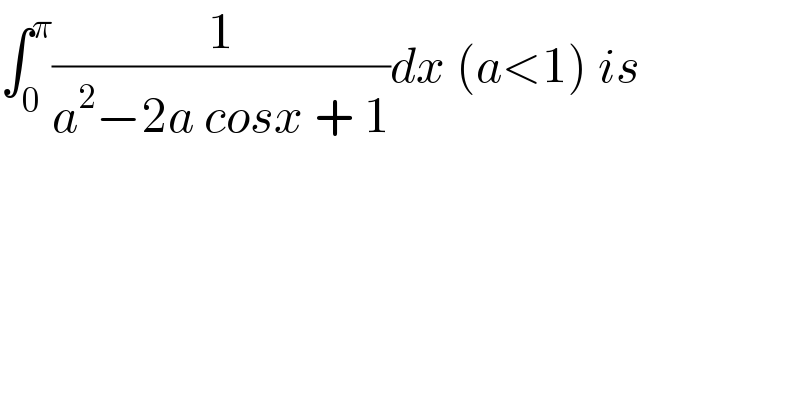
∫_0 ^π (1/(a^2 −2a cosx + 1))dx (a<1) is

$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{2}{a}\:{cosx}\:+\:\mathrm{1}}{dx}\:\left({a}<\mathrm{1}\right)\:{is} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 03/Jul/20

f(a) =∫_0 ^π (dx/(a^2 −2acosx +1)) changement tan((x/2))=t give f(a) =∫_0 ^∞ ((2dt)/((1+t^2 )(a^2 −2a×((1−t^2 )/(1+t^2 )) +1))) =∫_0 ^∞ ((2dt)/(a^2 +a^2 t^2 −2a+2at^2 +1+t^2 )) =∫_0 ^∞ ((2dt)/((a^2 +2a+1)t^2 +a^2 −2a+1)) =(2/((a+1)^2 ))∫_0 ^∞ (dt/(t^2 +(((a−1)^2 )/((a+1)^2 )))) =(2/((a+1)^2 ))∫_0 ^∞ (dt/(t^(2 ) +(((a−1)/(a+1)))^2 )) =_(t =((1−a)/(1+a))u) (2/((a+1)^2 )) ∫_0 ^∞ (1/((((1−a)/(1+a)))^2 (1+u^2 )))×((1−a)/(1+a))du =(2/((1+a)^2 ))×(((1+a)^2 )/((1−a)^2 ))×((1−a)/(1+a)) ∫_0 ^∞ (du/(1+u^2 )) =(2/(1−a^2 ))×(π/2) =(π/(1−a^2 )) ⇒f(a) =(π/(1−a^2 ))

$$\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dx}}{\mathrm{a}^{\mathrm{2}} −\mathrm{2acosx}\:+\mathrm{1}}\:\:\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{2a}×\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:+\mathrm{1}\right)}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2dt}}{\mathrm{a}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} −\mathrm{2a}+\mathrm{2at}^{\mathrm{2}} +\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2dt}}{\left(\mathrm{a}^{\mathrm{2}} \:+\mathrm{2a}+\mathrm{1}\right)\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \:−\mathrm{2a}+\mathrm{1}}\:=\frac{\mathrm{2}}{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} \:+\frac{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}\:} \:+\left(\frac{\mathrm{a}−\mathrm{1}}{\mathrm{a}+\mathrm{1}}\right)^{\mathrm{2}} }\:\:=_{\mathrm{t}\:=\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}\mathrm{u}} \:\:\:\frac{\mathrm{2}}{\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left(\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}\right)^{\mathrm{2}} \left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)}×\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}\mathrm{du} \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{a}\right)^{\mathrm{2}} }×\frac{\left(\mathrm{1}+\mathrm{a}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{a}\right)^{\mathrm{2}} }×\frac{\mathrm{1}−\mathrm{a}}{\mathrm{1}+\mathrm{a}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\pi}{\mathrm{1}−\mathrm{a}^{\mathrm{2}} } \\ $$

Commented by Rohit@Thakur last updated on 04/Jul/20

Thank you sir

$${Thank}\:{you}\:{sir} \\ $$

Commented by mathmax by abdo last updated on 04/Jul/20

you are welcome sir.

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com