
Question Number 54972 by peter frank last updated on 15/Feb/19
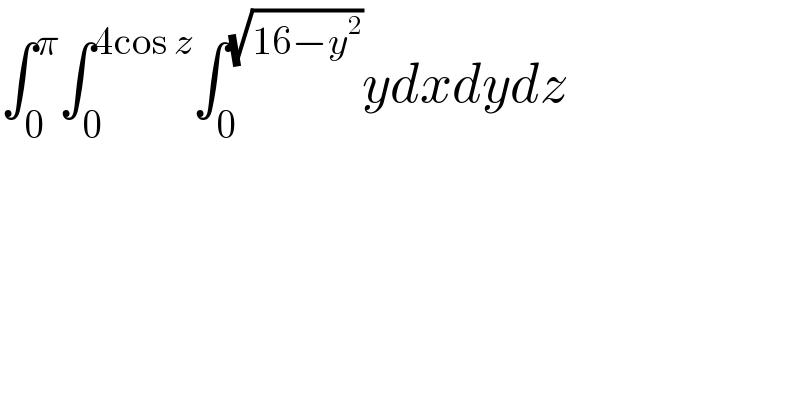
$$\int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\mathrm{4cos}\:{z}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{16}−{y}^{\mathrm{2}} }} {ydxdydz} \\ $$
Answered by kaivan.ahmadi last updated on 15/Feb/19
![∫_0 ^π ∫_0 ^(4cosz) y x]_0 ^(√(16−y^2 )) dydz= ∫_0 ^π ∫_0 ^(4cosz) (y(√(16−y^2 )))dydz= ∫_0 ^π ((−1)/3)(16−y^2 )^(3/2) ]_0 ^(4cosz) dz= ((−1)/3)∫_0 ^π ((16−16cos^2 z)^(3/2) −16^(3/2) )dz= ((−16^(3/2) )/3)∫_0 ^π (sin^3 z−1)dz=((−16^(3/2) )/3)×(((sin^2 zcosz+2cosz)/3)−z)_0 ^π = ((16^(3/2) )/3)×[(((−2)/3)−π)−((2/3))]= ((−16^(3/2) )/3)×(((−4)/3)−π)=((256)/9)+((64)/3)π](Q54976.png)
$$\left.\int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\mathrm{4}{cosz}} {y}\:{x}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{16}−{y}^{\mathrm{2}} }} {dydz}= \\ $$$$\int_{\mathrm{0}} ^{\pi} \int_{\mathrm{0}} ^{\mathrm{4}{cosz}} \left({y}\sqrt{\mathrm{16}−{y}^{\mathrm{2}} }\right){dydz}= \\ $$$$\left.\int_{\mathrm{0}} ^{\pi} \frac{−\mathrm{1}}{\mathrm{3}}\left(\mathrm{16}−{y}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{4}{cosz}} {dz}= \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\pi} \left(\left(\mathrm{16}−\mathrm{16}{cos}^{\mathrm{2}} {z}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{16}^{\frac{\mathrm{3}}{\mathrm{2}}} \right){dz}= \\ $$$$\frac{−\mathrm{16}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}\int_{\mathrm{0}} ^{\pi} \left({sin}^{\mathrm{3}} {z}−\mathrm{1}\right){dz}=\frac{−\mathrm{16}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}×\left(\frac{{sin}^{\mathrm{2}} {zcosz}+\mathrm{2}{cosz}}{\mathrm{3}}−{z}\right)_{\mathrm{0}} ^{\pi} = \\ $$$$\frac{\mathrm{16}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}×\left[\left(\frac{−\mathrm{2}}{\mathrm{3}}−\pi\right)−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\right]= \\ $$$$\frac{−\mathrm{16}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{3}}×\left(\frac{−\mathrm{4}}{\mathrm{3}}−\pi\right)=\frac{\mathrm{256}}{\mathrm{9}}+\frac{\mathrm{64}}{\mathrm{3}}\pi \\ $$$$ \\ $$$$ \\ $$
