
Question Number 210060 by SANOGO last updated on 29/Jul/24
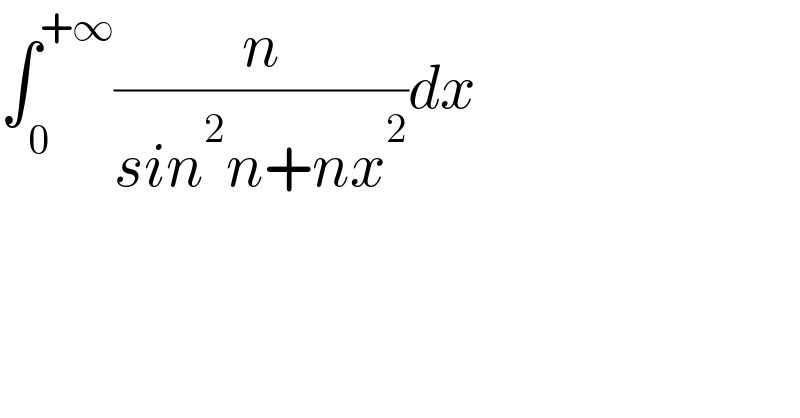
$$\int_{\mathrm{0}} ^{+\infty} \frac{{n}}{{sin}^{\mathrm{2}} {n}+{nx}^{\mathrm{2}} }{dx} \\ $$$$ \\ $$
Answered by mr W last updated on 29/Jul/24
![=∫_0 ^(+∞) (dx/((((sin n)/( (√n))))^2 +x^2 )) =((√n)/(∣sin n∣))[tan^(−1) (((√n)x)/(∣sin n∣))]_0 ^(+∞) =((√n)/(∣sin n∣))×(π/2) =((π(√n))/(2∣sin n∣))](Q210062.png)
$$=\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{\left(\frac{\mathrm{sin}\:{n}}{\:\sqrt{{n}}}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$=\frac{\sqrt{{n}}}{\mid\mathrm{sin}\:{n}\mid}\left[\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{{n}}{x}}{\mid\mathrm{sin}\:{n}\mid}\overset{+\infty} {\right]}_{\mathrm{0}} \\ $$$$=\frac{\sqrt{{n}}}{\mid\mathrm{sin}\:{n}\mid}×\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{\pi\sqrt{{n}}}{\mathrm{2}\mid\mathrm{sin}\:{n}\mid} \\ $$
Commented by klipto last updated on 29/Jul/24

$$\boldsymbol{\mathrm{hot}}\:\boldsymbol{\mathrm{man}}\: \\ $$
