Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 219911 by Nicholas666 last updated on 03/May/25

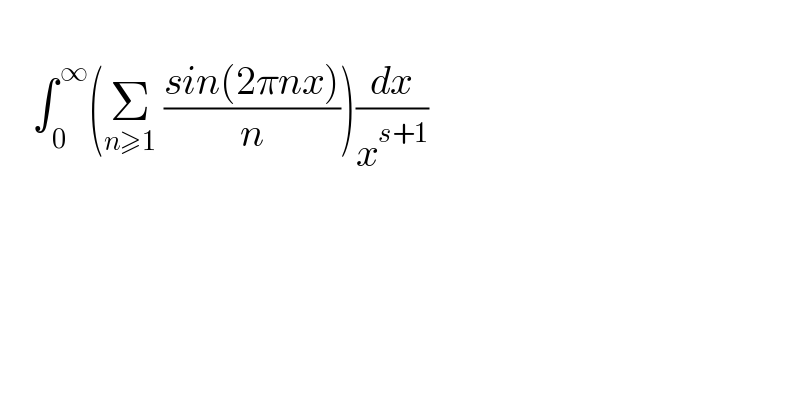
∫_( 0) ^( ∞) (Σ_(n≥1) ((sin(2πnx))/n))(dx/x^(s+1) )

$$ \\ $$$$\:\:\:\:\int_{\:\mathrm{0}} ^{\:\infty} \left(\underset{{n}\geqslant\mathrm{1}} {\sum}\:\frac{{sin}\left(\mathrm{2}\pi{nx}\right)}{{n}}\right)\frac{{dx}}{{x}^{{s}+\mathrm{1}} } \\ $$$$ \\ $$

Commented by MrGaster last updated on 03/May/25

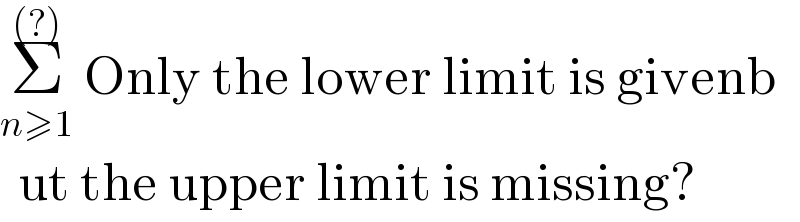
Σ_(n≥1) ^((?)) Only the lower limit is givenb ut the upper limit is missing?

$$\underset{{n}\geqslant\mathrm{1}} {\overset{\left(?\right)} {\sum}}\:\mathrm{Only}\:\mathrm{the}\:\mathrm{lower}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{givenb} \\ $$$$\mathrm{ut}\:\mathrm{the}\:\mathrm{upper}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{missing}? \\ $$

Answered by MrGaster last updated on 03/May/25

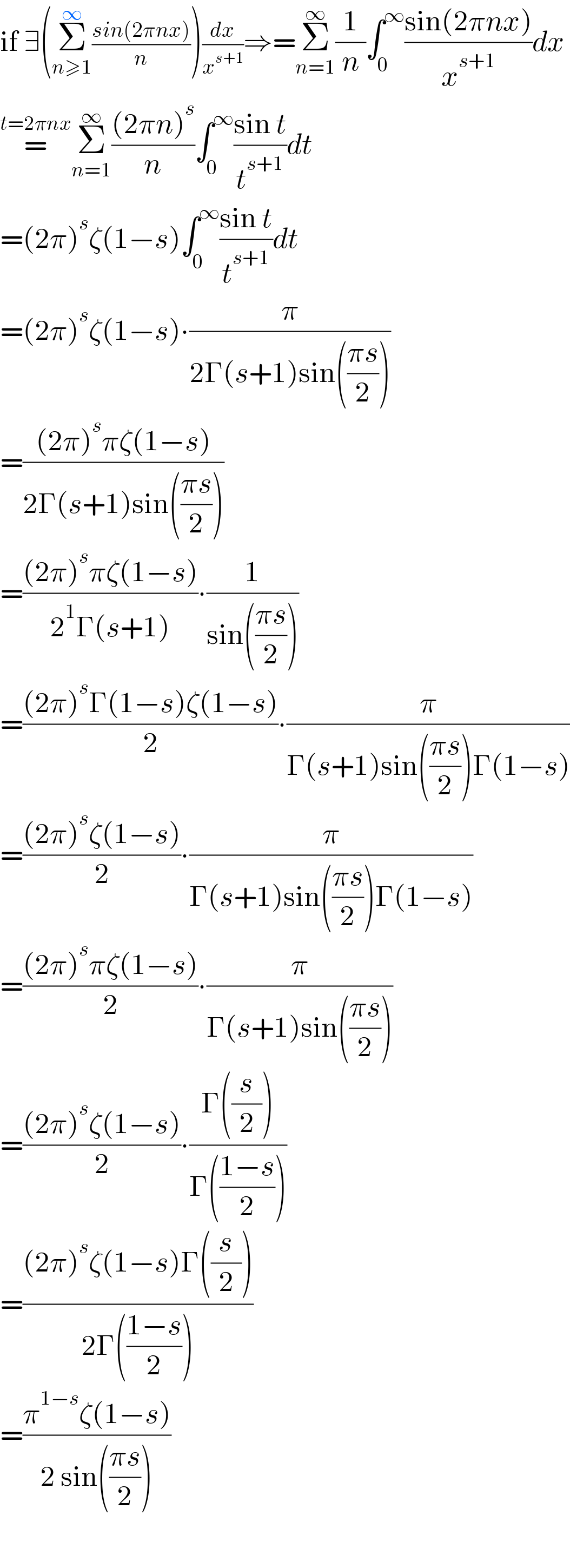
if ∃(Σ_(n≥1) ^∞ ((sin(2πnx))/n))(dx/x^(s+1) )⇒=Σ_(n=1) ^∞ (1/n)∫_0 ^∞ ((sin(2πnx))/x^(s+1) )dx =^(t=2πnx) Σ_(n=1) ^∞ (((2πn)^s )/n)∫_0 ^∞ ((sin t)/t^(s+1) )dt =(2π)^s ζ(1−s)∫_0 ^∞ ((sin t)/t^(s+1) )dt =(2π)^s ζ(1−s)∙(π/(2Γ(s+1)sin(((πs)/2)))) =(((2π)^s πζ(1−s))/(2Γ(s+1)sin(((πs)/2)))) =(((2π)^s πζ(1−s))/(2^1 Γ(s+1)))∙(1/(sin(((πs)/2)))) =(((2π)^s Γ(1−s)ζ(1−s))/2)∙(π/(Γ(s+1)sin(((πs)/2))Γ(1−s))) =(((2π)^s ζ(1−s))/2)∙(π/(Γ(s+1)sin(((πs)/2))Γ(1−s))) =(((2π)^s πζ(1−s))/2)∙(π/(Γ(s+1)sin(((πs)/2)))) =(((2π)^s ζ(1−s))/2)∙((Γ((s/2)))/(Γ(((1−s)/2)))) =(((2π)^s ζ(1−s)Γ((s/2)))/(2Γ(((1−s)/2)))) =((π^(1−s) ζ(1−s))/(2 sin(((πs)/2))))

$$\mathrm{if}\:\exists\left(\underset{{n}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{{sin}\left(\mathrm{2}\pi{nx}\right)}{{n}}\right)\frac{{dx}}{{x}^{{s}+\mathrm{1}} }\Rightarrow=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\left(\mathrm{2}\pi{nx}\right)}{{x}^{{s}+\mathrm{1}} }{dx} \\ $$$$\overset{{t}=\mathrm{2}\pi{nx}} {=}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(\mathrm{2}\pi{n}\right)^{{s}} }{{n}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:{t}}{{t}^{{s}+\mathrm{1}} }{dt} \\ $$$$=\left(\mathrm{2}\pi\right)^{{s}} \zeta\left(\mathrm{1}−{s}\right)\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:{t}}{{t}^{{s}+\mathrm{1}} }{dt} \\ $$$$=\left(\mathrm{2}\pi\right)^{{s}} \zeta\left(\mathrm{1}−{s}\right)\centerdot\frac{\pi}{\mathrm{2}\Gamma\left({s}+\mathrm{1}\right)\mathrm{sin}\left(\frac{\pi{s}}{\mathrm{2}}\right)} \\ $$$$=\frac{\left(\mathrm{2}\pi\right)^{{s}} \pi\zeta\left(\mathrm{1}−{s}\right)}{\mathrm{2}\Gamma\left({s}+\mathrm{1}\right)\mathrm{sin}\left(\frac{\pi{s}}{\mathrm{2}}\right)} \\ $$$$=\frac{\left(\mathrm{2}\pi\right)^{{s}} \pi\zeta\left(\mathrm{1}−{s}\right)}{\mathrm{2}^{\mathrm{1}} \Gamma\left({s}+\mathrm{1}\right)}\centerdot\frac{\mathrm{1}}{\mathrm{sin}\left(\frac{\pi{s}}{\mathrm{2}}\right)} \\ $$$$=\frac{\left(\mathrm{2}\pi\right)^{{s}} \Gamma\left(\mathrm{1}−{s}\right)\zeta\left(\mathrm{1}−{s}\right)}{\mathrm{2}}\centerdot\frac{\pi}{\Gamma\left({s}+\mathrm{1}\right)\mathrm{sin}\left(\frac{\pi{s}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−{s}\right)} \\ $$$$=\frac{\left(\mathrm{2}\pi\right)^{{s}} \zeta\left(\mathrm{1}−{s}\right)}{\mathrm{2}}\centerdot\frac{\pi}{\Gamma\left({s}+\mathrm{1}\right)\mathrm{sin}\left(\frac{\pi{s}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−{s}\right)} \\ $$$$=\frac{\left(\mathrm{2}\pi\right)^{{s}} \pi\zeta\left(\mathrm{1}−{s}\right)}{\mathrm{2}}\centerdot\frac{\pi}{\Gamma\left({s}+\mathrm{1}\right)\mathrm{sin}\left(\frac{\pi{s}}{\mathrm{2}}\right)} \\ $$$$=\frac{\left(\mathrm{2}\pi\right)^{{s}} \zeta\left(\mathrm{1}−{s}\right)}{\mathrm{2}}\centerdot\frac{\Gamma\left(\frac{{s}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{1}−{s}}{\mathrm{2}}\right)} \\ $$$$=\frac{\left(\mathrm{2}\pi\right)^{{s}} \zeta\left(\mathrm{1}−{s}\right)\Gamma\left(\frac{{s}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{\mathrm{1}−{s}}{\mathrm{2}}\right)} \\ $$$$=\frac{\pi^{\mathrm{1}−{s}} \zeta\left(\mathrm{1}−{s}\right)}{\mathrm{2}\:\mathrm{sin}\left(\frac{\pi{s}}{\mathrm{2}}\right)} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com