Question and Answers Forum

All Questions      Topic List

Logarithms Questions

Previous in All Question      Next in All Question      

Previous in Logarithms      Next in Logarithms      

Question Number 196026 by Erico last updated on 16/Aug/23

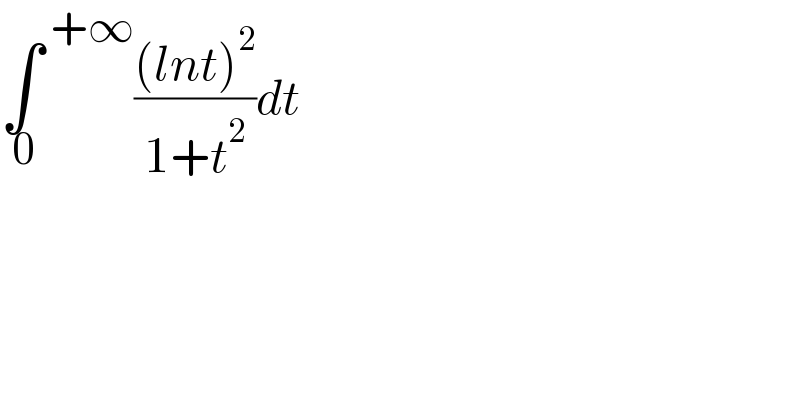
∫^( +∞) _( 0) (((lnt)^2 )/(1+t^2 ))dt

$$\underset{\:\mathrm{0}} {\int}^{\:+\infty} \frac{\left({lnt}\right)^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$

Answered by sniper237 last updated on 16/Aug/23

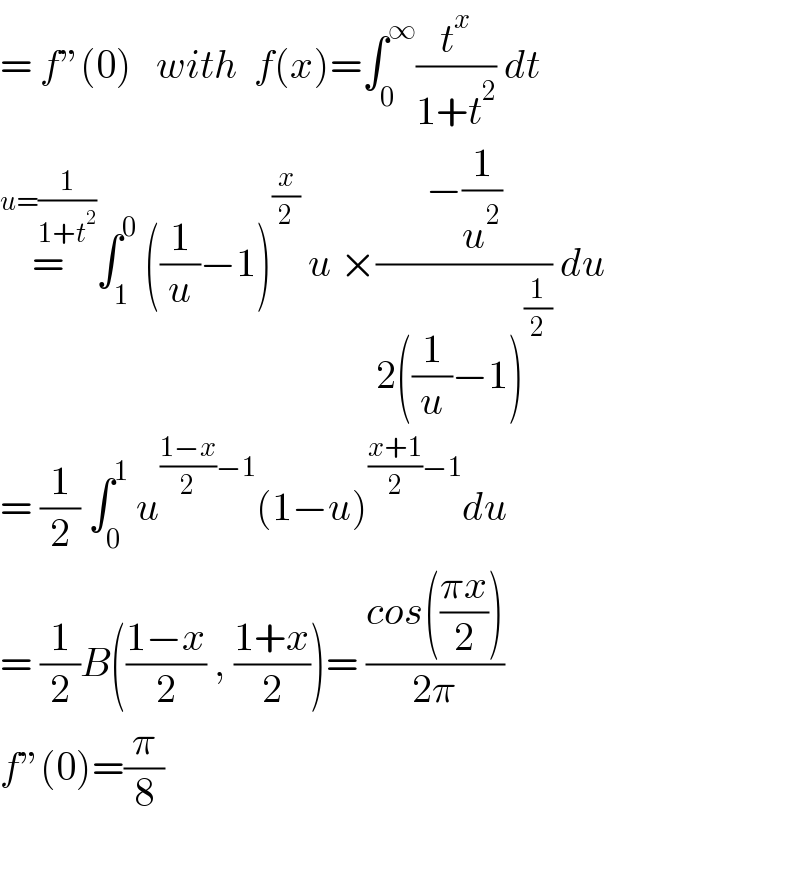
= f”(0) with f(x)=∫_0 ^∞ (t^x /(1+t^2 )) dt =^(u=(1/(1+t^2 ))) ∫_1 ^0 ((1/u)−1)^(x/2) u ×((−(1/u^2 ))/(2((1/u)−1)^(1/2) )) du = (1/2) ∫_0 ^1 u^(((1−x)/2)−1) (1−u)^(((x+1)/2)−1) du = (1/2)B(((1−x)/2) , ((1+x)/2))= ((cos(((πx)/2)))/(2π)) f”(0)=(π/8)

$$=\:{f}''\left(\mathrm{0}\right)\:\:\:{with}\:\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$$\overset{{u}=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }} {=}\int_{\mathrm{1}} ^{\mathrm{0}} \:\left(\frac{\mathrm{1}}{{u}}−\mathrm{1}\right)^{\frac{{x}}{\mathrm{2}}} \:{u}\:×\frac{−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}{\mathrm{2}\left(\frac{\mathrm{1}}{{u}}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\:{du} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{u}^{\frac{\mathrm{1}−{x}}{\mathrm{2}}−\mathrm{1}} \left(\mathrm{1}−{u}\right)^{\frac{{x}+\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {du} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}{B}\left(\frac{\mathrm{1}−{x}}{\mathrm{2}}\:,\:\frac{\mathrm{1}+{x}}{\mathrm{2}}\right)=\:\frac{{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)}{\mathrm{2}\pi} \\ $$$${f}''\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{8}} \\ $$$$ \\ $$

Commented by York12 last updated on 16/Aug/23

Great !!

$${Great}\:!! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com