
Question Number 84242 by Rio Michael last updated on 10/Mar/20
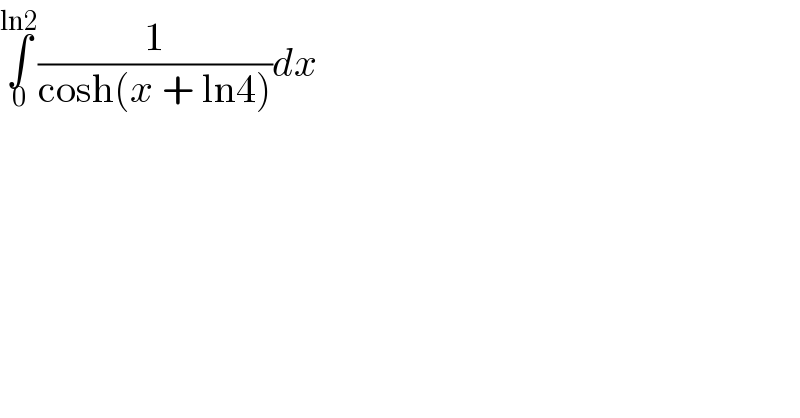
$$\underset{\mathrm{0}} {\overset{\mathrm{ln2}} {\int}}\frac{\mathrm{1}}{\mathrm{cosh}\left({x}\:+\:\mathrm{ln4}\right)}{dx} \\ $$
Commented by mathmax by abdo last updated on 10/Mar/20
![I =∫_0 ^(ln(2)) (1/(ch(x+ln4)))dx ⇒I =_(x+ln4=t) ∫_(2ln(2)) ^(3ln(2)) (dt/(ch(t))) =2 ∫_(2ln(2)) ^(3ln(2)) (dt/(e^t +e^(−t) )) =_(e^t =u) 2 ∫_4 ^8 (du/(u(u+u^(−1) ))) =2∫_4 ^8 (du/(u^2 +1)) =2[arctanu]_4 ^8 =2(arctan(8)−arctan(4))](Q84271.png)
$${I}\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \:\frac{\mathrm{1}}{{ch}\left({x}+{ln}\mathrm{4}\right)}{dx}\:\Rightarrow{I}\:=_{{x}+{ln}\mathrm{4}={t}} \:\:\int_{\mathrm{2}{ln}\left(\mathrm{2}\right)} ^{\mathrm{3}{ln}\left(\mathrm{2}\right)} \:\:\frac{{dt}}{{ch}\left({t}\right)} \\ $$$$=\mathrm{2}\:\int_{\mathrm{2}{ln}\left(\mathrm{2}\right)} ^{\mathrm{3}{ln}\left(\mathrm{2}\right)} \:\frac{{dt}}{{e}^{{t}} \:+{e}^{−{t}} }\:=_{{e}^{{t}} ={u}} \:\:\mathrm{2}\:\int_{\mathrm{4}} ^{\mathrm{8}} \:\frac{{du}}{{u}\left({u}+{u}^{−\mathrm{1}} \right)}\:=\mathrm{2}\int_{\mathrm{4}} ^{\mathrm{8}} \:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\mathrm{2}\left[{arctanu}\right]_{\mathrm{4}} ^{\mathrm{8}} \:=\mathrm{2}\left({arctan}\left(\mathrm{8}\right)−{arctan}\left(\mathrm{4}\right)\right) \\ $$
Answered by TANMAY PANACEA last updated on 10/Mar/20
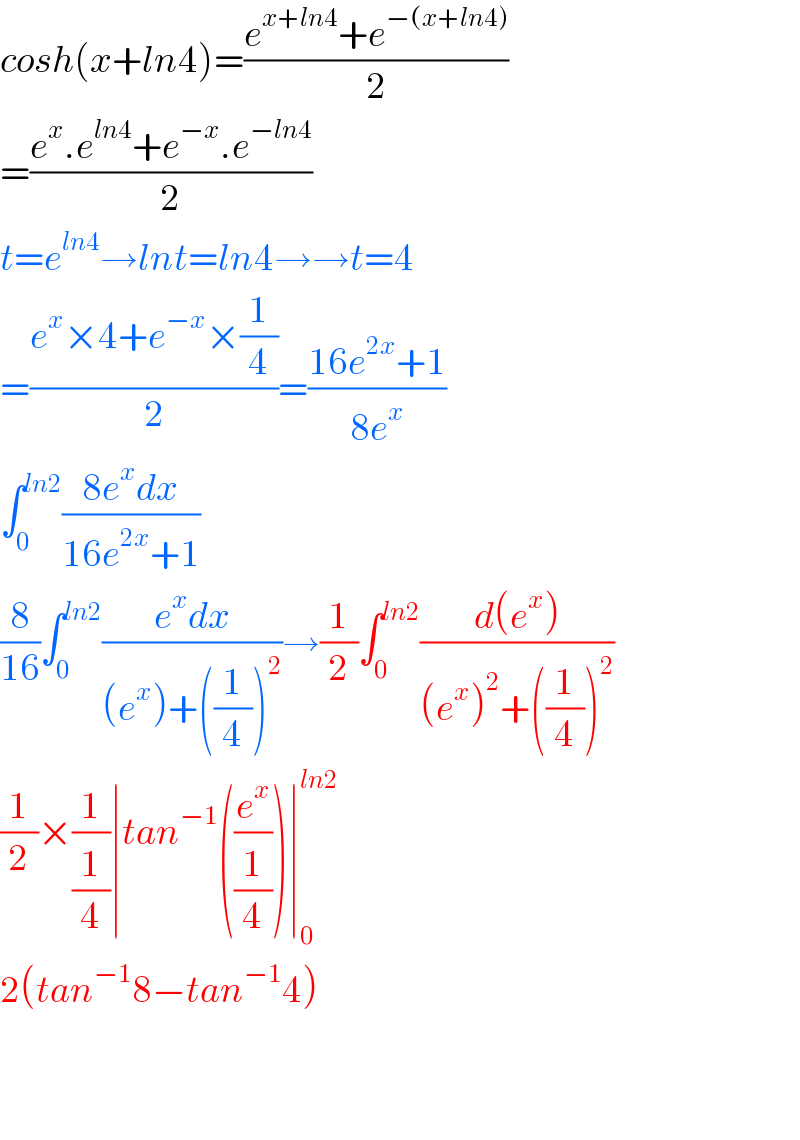
$${cosh}\left({x}+{ln}\mathrm{4}\right)=\frac{{e}^{{x}+{ln}\mathrm{4}} +{e}^{−\left({x}+{ln}\mathrm{4}\right)} }{\mathrm{2}} \\ $$$$=\frac{{e}^{{x}} .{e}^{{ln}\mathrm{4}} +{e}^{−{x}} .{e}^{−{ln}\mathrm{4}} }{\mathrm{2}} \\ $$$${t}={e}^{{ln}\mathrm{4}} \rightarrow{lnt}={ln}\mathrm{4}\rightarrow\rightarrow{t}=\mathrm{4} \\ $$$$=\frac{{e}^{{x}} ×\mathrm{4}+{e}^{−{x}} ×\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{16}{e}^{\mathrm{2}{x}} +\mathrm{1}}{\mathrm{8}{e}^{{x}} } \\ $$$$\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \frac{\mathrm{8}{e}^{{x}} {dx}}{\mathrm{16}{e}^{\mathrm{2}{x}} +\mathrm{1}} \\ $$$$\frac{\mathrm{8}}{\mathrm{16}}\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \frac{{e}^{{x}} {dx}}{\left({e}^{{x}} \right)+\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} }\rightarrow\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{ln}\mathrm{2}} \frac{{d}\left({e}^{{x}} \right)}{\left({e}^{{x}} \right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{4}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{e}^{{x}} }{\frac{\mathrm{1}}{\mathrm{4}}}\right)\mid_{\mathrm{0}} ^{{ln}\mathrm{2}} \\ $$$$\mathrm{2}\left({tan}^{−\mathrm{1}} \mathrm{8}−{tan}^{−\mathrm{1}} \mathrm{4}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Rio Michael last updated on 10/Mar/20

$$\mathrm{thanks} \\ $$
