
Question Number 117811 by Lordose last updated on 13/Oct/20
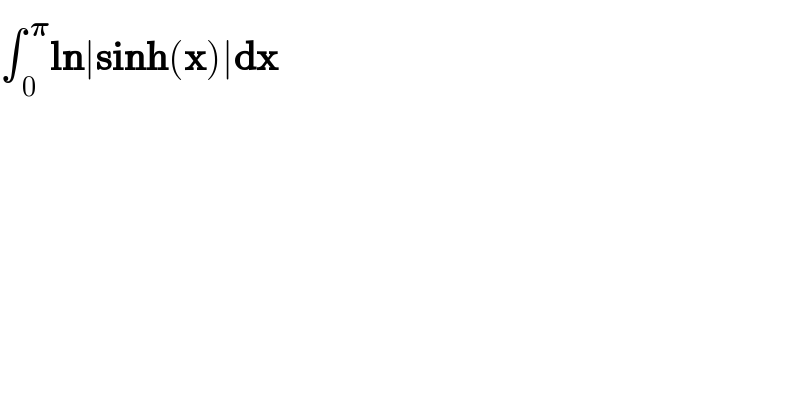
$$\int_{\:\mathrm{0}} ^{\:\boldsymbol{\pi}} \boldsymbol{\mathrm{ln}}\mid\boldsymbol{\mathrm{sinh}}\left(\boldsymbol{\mathrm{x}}\right)\mid\boldsymbol{\mathrm{dx}} \\ $$
Answered by mindispower last updated on 13/Oct/20
![=∫_0 ^π ln(sh(x))dx sh(x)=((e^x −e^(−x) )/2) =∫_0 ^π (ln(e^x (1−e^(−2x) ))−ln(2))dx =∫_0 ^π (x+ln(1−e^(−2x) )−ln(2))dx =[(1/2)x^2 −xln(2)]_0 ^π _(=A) +∫_0 ^π (ln(1−e^(−2x) )dx)_(=B) ln(1−e^(−2x) )=−Σ_(n≥0) (e^(−2(n+1x) /(n+1)) ∫_0 ^π ln(1−e^(−2x) )dx=−Σ_(n≥0) (1/(n+1))∫_0 ^π e^(−2(n+)x) dx Σ_(n≥0) ((e^(−2(n+1)π) −1)/(2(n+1)^2 ))=Σ_(n≥1) (((e^(−2π) )^n )/n^2 )−Σ_(n≥1) (1/(2n^2 )) Li_s (x)=Σ_(k≥1) (x^k /k^s ) we get=(1/2)(Li_2 (e^(−2π) )−Li_2 (1))=(1/2)Li_2 (e^(−2π) )−(1/2)ζ(2) =(1/2)Li_2 (e^(−2π) )−(π^2 /(12)) A=(1/2)π^2 −πln(2) A+B=((5π^2 )/(12))−πln(2)+Li_2 (e^(−2π) ) ∫_0 ^π ln(sh(x))dx=((5π^2 )/(12))−πln(2)+Li_2 (e^(−2π) )](Q117815.png)
$$=\int_{\mathrm{0}} ^{\pi} {ln}\left({sh}\left({x}\right)\right){dx} \\ $$$${sh}\left({x}\right)=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \left({ln}\left({e}^{{x}} \:\left(\mathrm{1}−{e}^{−\mathrm{2}{x}} \right)\right)−{ln}\left(\mathrm{2}\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \left({x}+{ln}\left(\mathrm{1}−{e}^{−\mathrm{2}{x}} \right)−{ln}\left(\mathrm{2}\right)\right){dx} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −{xln}\left(\mathrm{2}\right)\right]_{\mathrm{0}} ^{\pi} \:\underset{={A}} {\:}+\int_{\mathrm{0}} ^{\pi} \left({ln}\left(\mathrm{1}−{e}^{−\mathrm{2}{x}} \right){dx}\underset{={B}} {\right)} \\ $$$${ln}\left(\mathrm{1}−{e}^{−\mathrm{2}{x}} \right)=−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{e}^{−\mathrm{2}\left({n}+\mathrm{1}{x}\right.} }{{n}+\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\pi} {ln}\left(\mathrm{1}−{e}^{−\mathrm{2}{x}} \right){dx}=−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\pi} {e}^{−\mathrm{2}\left({n}+\right){x}} {dx} \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{e}^{−\mathrm{2}\left({n}+\mathrm{1}\right)\pi} −\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left({e}^{−\mathrm{2}\pi} \right)^{{n}} }{{n}^{\mathrm{2}} }−\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} } \\ $$$${Li}_{{s}} \left({x}\right)=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{x}^{{k}} }{{k}^{{s}} } \\ $$$${we}\:{get}=\frac{\mathrm{1}}{\mathrm{2}}\left({Li}_{\mathrm{2}} \left({e}^{−\mathrm{2}\pi} \right)−{Li}_{\mathrm{2}} \left(\mathrm{1}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left({e}^{−\mathrm{2}\pi} \right)−\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\mathrm{2}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{Li}_{\mathrm{2}} \left({e}^{−\mathrm{2}\pi} \right)−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\pi^{\mathrm{2}} −\pi{ln}\left(\mathrm{2}\right) \\ $$$${A}+{B}=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{12}}−\pi{ln}\left(\mathrm{2}\right)+{Li}_{\mathrm{2}} \left({e}^{−\mathrm{2}\pi} \right) \\ $$$$\int_{\mathrm{0}} ^{\pi} {ln}\left({sh}\left({x}\right)\right){dx}=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{12}}−\pi{ln}\left(\mathrm{2}\right)+{Li}_{\mathrm{2}} \left({e}^{−\mathrm{2}\pi} \right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
