Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 154202 by mathdanisur last updated on 15/Sep/21

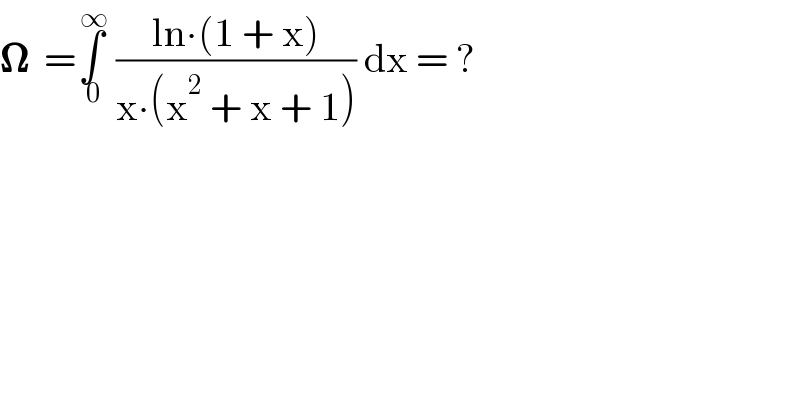
𝛀 =∫_( 0) ^( ∞) ((ln∙(1 + x))/(x∙(x^2 + x + 1))) dx = ?

$$\boldsymbol{\Omega}\:\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{ln}\centerdot\left(\mathrm{1}\:+\:\mathrm{x}\right)}{\mathrm{x}\centerdot\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\mathrm{1}\right)}\:\mathrm{dx}\:=\:? \\ $$

Answered by qaz last updated on 15/Sep/21

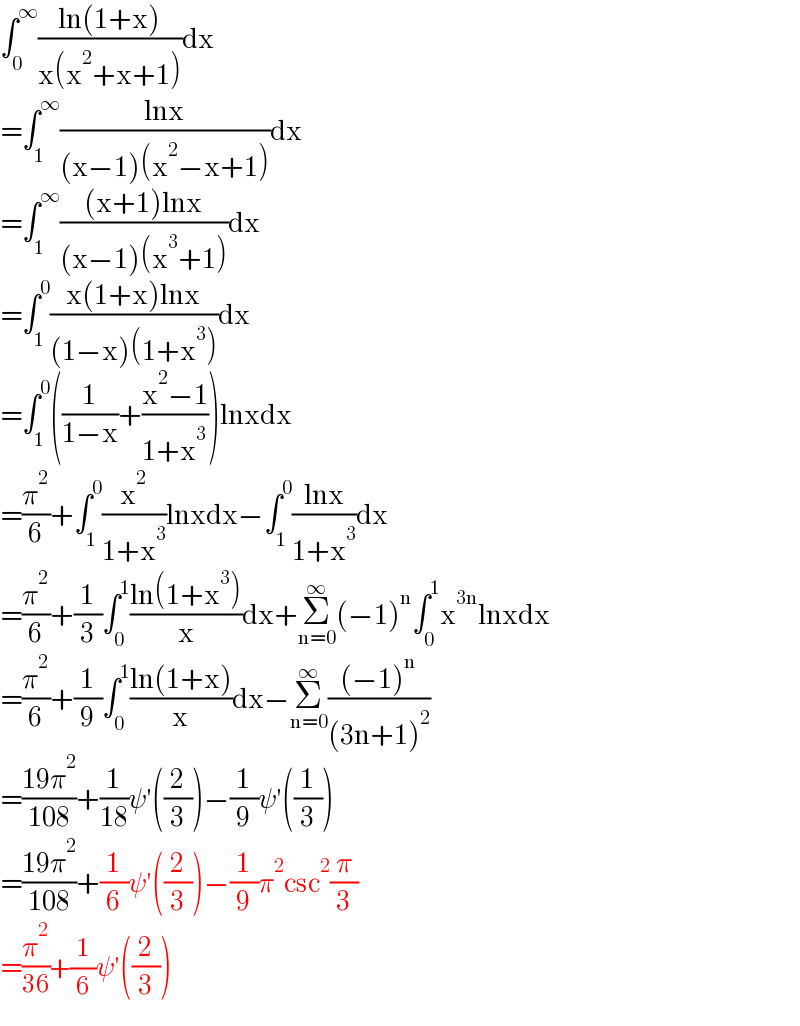
∫_0 ^∞ ((ln(1+x))/(x(x^2 +x+1)))dx =∫_1 ^∞ ((lnx)/((x−1)(x^2 −x+1)))dx =∫_1 ^∞ (((x+1)lnx)/((x−1)(x^3 +1)))dx =∫_1 ^0 ((x(1+x)lnx)/((1−x)(1+x^3 )))dx =∫_1 ^0 ((1/(1−x))+((x^2 −1)/(1+x^3 )))lnxdx =(π^2 /6)+∫_1 ^0 (x^2 /(1+x^3 ))lnxdx−∫_1 ^0 ((lnx)/(1+x^3 ))dx =(π^2 /6)+(1/3)∫_0 ^1 ((ln(1+x^3 ))/x)dx+Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(3n) lnxdx =(π^2 /6)+(1/9)∫_0 ^1 ((ln(1+x))/x)dx−Σ_(n=0) ^∞ (((−1)^n )/((3n+1)^2 )) =((19π^2 )/(108))+(1/(18))ψ′((2/3))−(1/9)ψ′((1/3)) =((19π^2 )/(108))+(1/6)ψ′((2/3))−(1/9)π^2 csc^2 (π/3) =(π^2 /(36))+(1/6)ψ′((2/3))

$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{lnx}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{lnx}}{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{3}} +\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{lnx}}{\left(\mathrm{1}−\mathrm{x}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)}\mathrm{dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}+\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\right)\mathrm{lnxdx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{lnxdx}−\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{x}}\mathrm{dx}+\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{3n}} \mathrm{lnxdx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{9}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}−\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{3n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{19}\pi^{\mathrm{2}} }{\mathrm{108}}+\frac{\mathrm{1}}{\mathrm{18}}\psi'\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{9}}\psi'\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{19}\pi^{\mathrm{2}} }{\mathrm{108}}+\frac{\mathrm{1}}{\mathrm{6}}\psi'\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\frac{\mathrm{1}}{\mathrm{9}}\pi^{\mathrm{2}} \mathrm{csc}^{\mathrm{2}} \frac{\pi}{\mathrm{3}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{36}}+\frac{\mathrm{1}}{\mathrm{6}}\psi'\left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$

Commented by puissant last updated on 15/Sep/21

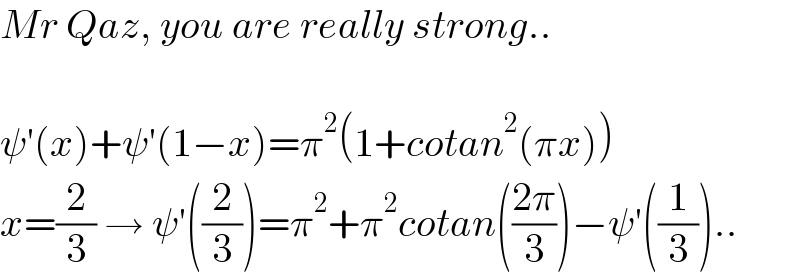
Mr Qaz, you are really strong.. ψ′(x)+ψ′(1−x)=π^2 (1+cotan^2 (πx)) x=(2/3) → ψ′((2/3))=π^2 +π^2 cotan(((2π)/3))−ψ′((1/3))..

$${Mr}\:{Qaz},\:{you}\:{are}\:{really}\:{strong}.. \\ $$$$ \\ $$$$\psi'\left({x}\right)+\psi'\left(\mathrm{1}−{x}\right)=\pi^{\mathrm{2}} \left(\mathrm{1}+{cotan}^{\mathrm{2}} \left(\pi{x}\right)\right) \\ $$$${x}=\frac{\mathrm{2}}{\mathrm{3}}\:\rightarrow\:\psi'\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=\pi^{\mathrm{2}} +\pi^{\mathrm{2}} {cotan}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−\psi'\left(\frac{\mathrm{1}}{\mathrm{3}}\right).. \\ $$

Commented by mathdanisur last updated on 15/Sep/21

Very nice Ser thank you

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$

Commented by mathdanisur last updated on 16/Sep/21

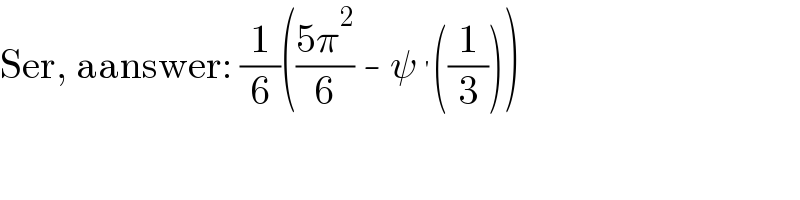
Ser, aanswer: (1/6)(((5π^2 )/6) - ψ^′ ((1/3)))

$$\mathrm{Ser},\:\mathrm{aanswer}:\:\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{6}}\:-\:\psi\:^{'} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com