
Question Number 172764 by Mathematification last updated on 01/Jul/22
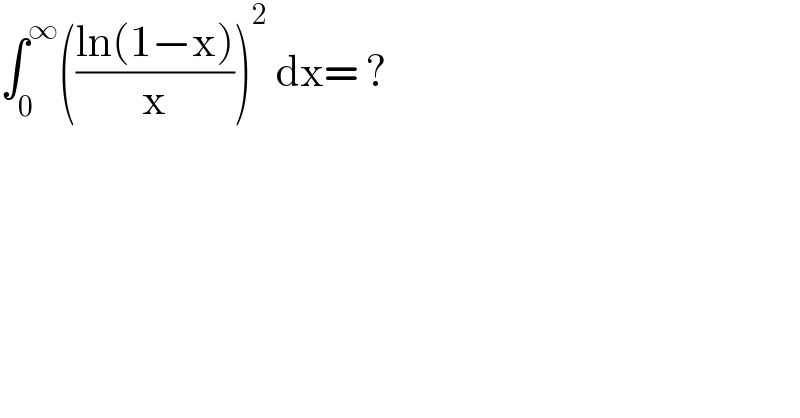
$$\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\right)^{\mathrm{2}} \:\mathrm{dx}=\:? \\ $$
Answered by Mathspace last updated on 01/Jul/22
![Υ=∫_0 ^∞ ((ln^2 (1−x))/x^2 )dx(u^′ =(1/x^2 )andv=ln^2 (1+x)) Υ=[−(1/x)ln^2 (1−x)]_0 ^(+∞) +∫_0 ^∞ (1/x)(−2)ln(1−x)dx =−2∫_0 ^∞ ((ln(1−x))/x)dx ln^′ (1−x)=−(1/(1−x))=−Σ_(n=0) ^∞ x^n ⇒ ln(1−x)=−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) +c(c=0) =−Σ_(n=1) ^∞ (x^n /n) ⇒−((ln(1−x))/x) =Σ_(n=1) ^∞ (x^(n−1) /n) ⇒ Υ=2Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^(n−1) dx =2Σ_(n=1) ^∞ (1/n^2 )=2.(π^2 /6)=(π^2 /3) Υ=(π^2 /3)](Q172781.png)
$$\Upsilon=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{{x}^{\mathrm{2}} }{dx}\left({u}^{'} =\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{andv}={ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)\right) \\ $$$$\Upsilon=\left[−\frac{\mathrm{1}}{{x}}{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}}\left(−\mathrm{2}\right){ln}\left(\mathrm{1}−{x}\right){dx} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$${ln}^{'} \left(\mathrm{1}−{x}\right)=−\frac{\mathrm{1}}{\mathrm{1}−{x}}=−\sum_{{n}=\mathrm{0}} ^{\infty} {x}^{{n}} \Rightarrow \\ $$$${ln}\left(\mathrm{1}−{x}\right)=−\sum_{{n}=\mathrm{0}} ^{\infty} \frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:+{c}\left({c}=\mathrm{0}\right) \\ $$$$=−\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{x}^{{n}} }{{n}}\:\Rightarrow−\frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{x}^{{n}−\mathrm{1}} }{{n}}\:\Rightarrow \\ $$$$\Upsilon=\mathrm{2}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}−\mathrm{1}} {dx} \\ $$$$=\mathrm{2}\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\mathrm{2}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Upsilon=\frac{\pi^{\mathrm{2}} }{\mathrm{3}} \\ $$
Commented by Mathematification last updated on 08/Jul/22
@Mathspace Please check the third and fourth line again sir.
