
Question Number 86728 by M±th+et£s last updated on 30/Mar/20
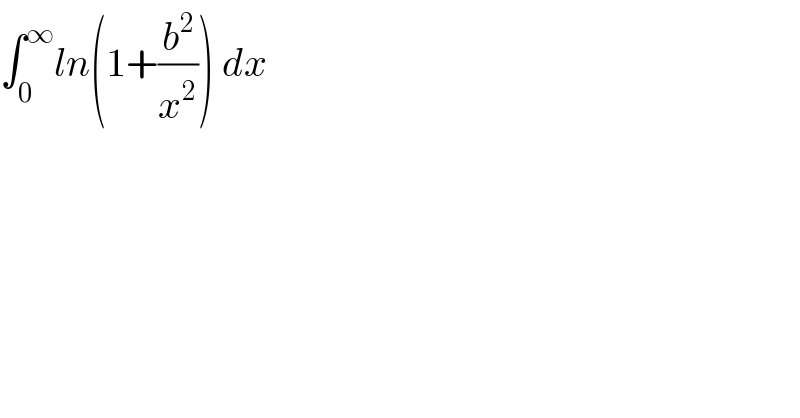
$$\int_{\mathrm{0}} ^{\infty} {ln}\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)\:{dx} \\ $$
Commented by mathmax by abdo last updated on 30/Mar/20

$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{ln}\left(\mathrm{1}+\frac{{a}}{{x}^{\mathrm{2}} }\right){dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{{a}}{{x}^{\mathrm{2}} }\right)}{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}^{\mathrm{2}} \:+{a}}\:=_{{x}=\sqrt{{a}}{u}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\sqrt{{a}}{du}}{{a}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\sqrt{{a}}}×\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\mathrm{2}\sqrt{{a}}}\:\Rightarrow{f}\left({a}\right)\:=\pi\sqrt{{a}}\:+{C} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}\:={C}\:\Rightarrow{f}\left({a}\right)\:=\pi\sqrt{{a}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{ln}\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right){dx}\:={f}\left({b}^{\mathrm{2}} \right)\:=\pi\mid{b}\mid \\ $$$$ \\ $$
