
Question Number 222317 by wewji12 last updated on 22/Jun/25
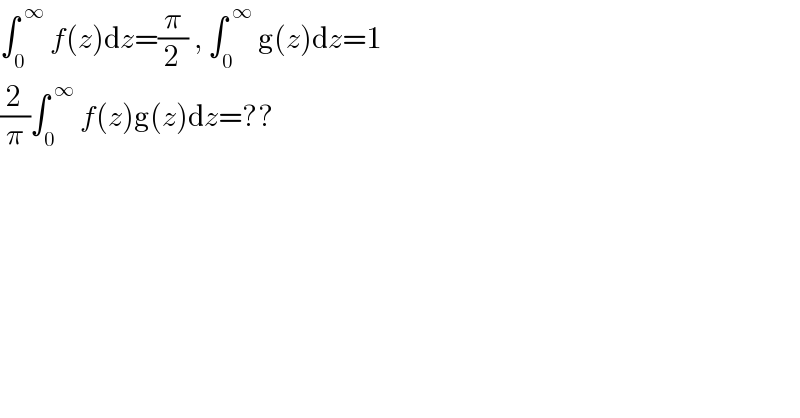
$$\int_{\mathrm{0}} ^{\:\infty} \:{f}\left({z}\right)\mathrm{d}{z}=\frac{\pi}{\mathrm{2}}\:,\:\int_{\mathrm{0}} ^{\:\infty} \:\mathrm{g}\left({z}\right)\mathrm{d}{z}=\mathrm{1} \\ $$$$\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\:\infty} \:{f}\left({z}\right)\mathrm{g}\left({z}\right)\mathrm{d}{z}=?? \\ $$
Answered by MrGaster last updated on 22/Jun/25
![∮_Σ F∙dS=∫∫∫_Ω ▽∙FdV F= (((f(z)g(z))),(0),(0) ),Σ={(x,y,z):x^2 +y^2 +z^2 =R^2 ,z≥0},R→∞ ▽∙F=(∂/∂z)(f(z)g(z)) ∫∫∫_Ω (∂/∂z)(f(z)g(z))dV=∫_0 ^∞ ∫_(−∞) ^∞ ∫_(−∞) ^∞ (∂/∂z)(f(z)g(z))dxdydz ▽∙F=(∂/∂z)(f(z)g(z)) ∫∫∫_Ω (∂/∂z)(f(z)g(z))=∫_0 ^∞ ∫_(−∞) ^∞ ∫_(−∞) ^∞ (∂/∂z)(f(z)g(z))dxdydz ∫_(−∞) ^∞ ∫_(−∞) ^∞ dxdx=πr^2 ,r=(√(x^2 +y^2 )) =π∫_0 ^∞ r^2 (∂/∂z)(f(z)g(z))drdz u=r^2 ,du=2rdr =(π/2)∫_0 ^∞ u(∂/∂z)(f(z)g(z))dufz L{(∂/∂z)(f(z)g(z))}=sL{f(z)g(z)}−f(0)g(0) f(0)=lim_(z→0) ((sin z)/z)=1,g(0)=e^0 =1 L{f(z)g(z)}=s arctan((1/s))−1 (π/2)∫_0 ^∞ e^(−sz) [s arctan((1/s))−]dz=(π/2)[arctan((1/s))−1]∫_0 ^∞ e^(−sz) dz ∫_0 ^∞ e^(−sz) dz=(1/s),s>0 =(π/2)[s arctan((1/s))−1](1/s)=(π/2)[arctan((1/s))−(1/s)] lim_(s→0^+ ) (π/2)[arctan((1/s))−(1/s)]=(π/2)[(π/2)−0]=(π^2 /4) (2/π)∫_0 ^∞ f(z)g(z)dz=(2/π)∙(π^2 /4)∙(1/π^(1/2) ) (2/π)∫_0 ^∞ f(z)g(z)=(1/2)](Q222319.png)
$$\oint_{\Sigma} \boldsymbol{\mathrm{F}}\centerdot{d}\boldsymbol{{S}}=\int\int\int_{\Omega} \bigtriangledown\centerdot\boldsymbol{\mathrm{F}}{dV} \\ $$$$\boldsymbol{\mathrm{F}}=\begin{pmatrix}{{f}\left({z}\right){g}\left({z}\right)}\\{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix},\Sigma=\left\{\left({x},{y},{z}\right):{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} ={R}^{\mathrm{2}} ,{z}\geq\mathrm{0}\right\},{R}\rightarrow\infty \\ $$$$\bigtriangledown\centerdot\boldsymbol{\mathrm{F}}=\frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right) \\ $$$$\int\int\int_{\Omega} \frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right)\mathrm{d}{V}=\int_{\mathrm{0}} ^{\infty} \int_{−\infty} ^{\infty} \int_{−\infty} ^{\infty} \frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right){dxdydz} \\ $$$$\bigtriangledown\centerdot\boldsymbol{\mathrm{F}}=\frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right) \\ $$$$\int\int\int_{\Omega} \frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right)=\int_{\mathrm{0}} ^{\infty} \int_{−\infty} ^{\infty} \int_{−\infty} ^{\infty} \frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right){dxdydz} \\ $$$$\int_{−\infty} ^{\infty} \int_{−\infty} ^{\infty} {dxdx}=\pi{r}^{\mathrm{2}} ,{r}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$=\pi\int_{\mathrm{0}} ^{\infty} {r}^{\mathrm{2}} \frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right){drdz} \\ $$$${u}={r}^{\mathrm{2}} ,{du}=\mathrm{2}{rdr} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {u}\frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right){dufz} \\ $$$$\mathscr{L}\left\{\frac{\partial}{\partial{z}}\left({f}\left({z}\right){g}\left({z}\right)\right)\right\}={s}\mathscr{L}\left\{{f}\left({z}\right){g}\left({z}\right)\right\}−{f}\left(\mathrm{0}\right){g}\left(\mathrm{0}\right) \\ $$$${f}\left(\mathrm{0}\right)=\underset{{z}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:{z}}{{z}}=\mathrm{1},{g}\left(\mathrm{0}\right)={e}^{\mathrm{0}} =\mathrm{1} \\ $$$$\mathscr{L}\left\{{f}\left({z}\right){g}\left({z}\right)\right\}={s}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{{s}}\right)−\mathrm{1} \\ $$$$\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{−{sz}} \left[{s}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{{s}}\right)−\right]\mathrm{d}{z}=\frac{\pi}{\mathrm{2}}\left[\mathrm{arctan}\left(\frac{\mathrm{1}}{{s}}\right)−\mathrm{1}\right]\int_{\mathrm{0}} ^{\infty} {e}^{−{sz}} {dz} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{sz}} {dz}=\frac{\mathrm{1}}{{s}},{s}>\mathrm{0} \\ $$$$=\frac{\pi}{\mathrm{2}}\left[{s}\:\mathrm{arctan}\left(\frac{\mathrm{1}}{{s}}\right)−\mathrm{1}\right]\frac{\mathrm{1}}{{s}}=\frac{\pi}{\mathrm{2}}\left[\mathrm{arctan}\left(\frac{\mathrm{1}}{{s}}\right)−\frac{\mathrm{1}}{{s}}\right] \\ $$$$\underset{{s}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\pi}{\mathrm{2}}\left[\mathrm{arctan}\left(\frac{\mathrm{1}}{{s}}\right)−\frac{\mathrm{1}}{{s}}\right]=\frac{\pi}{\mathrm{2}}\left[\frac{\pi}{\mathrm{2}}−\mathrm{0}\right]=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\infty} {f}\left({z}\right){g}\left({z}\right){dz}=\frac{\mathrm{2}}{\pi}\centerdot\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\centerdot\frac{\mathrm{1}}{\pi^{\mathrm{1}/\mathrm{2}} } \\ $$$$\frac{\mathrm{2}}{\pi}\int_{\mathrm{0}} ^{\infty} {f}\left({z}\right){g}\left({z}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
