
Question Number 119291 by 675480065 last updated on 23/Oct/20
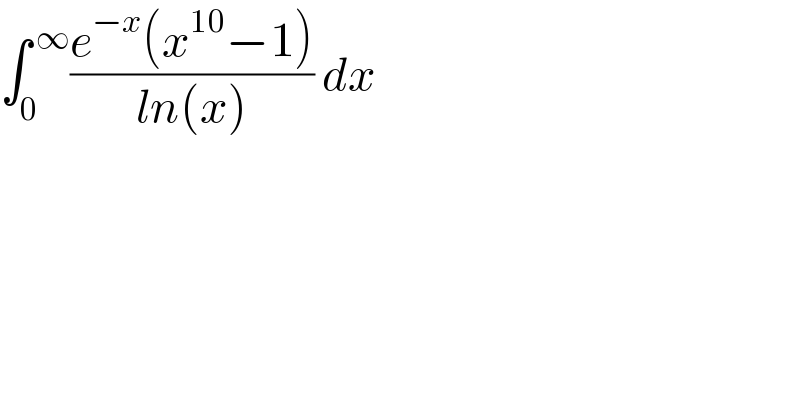
$$\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{−{x}} \left({x}^{\mathrm{10}} −\mathrm{1}\right)}{{ln}\left({x}\right)}\:{dx}\: \\ $$
Answered by TANMAY PANACEA last updated on 23/Oct/20

$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} \left({x}^{{a}} −\mathrm{1}\right)}{{lnx}}{dx} \\ $$$$\frac{{dI}\left({a}\right)}{{da}}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} ×{x}^{{a}} {lnx}}{{lnx}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {x}^{{a}+\mathrm{1}−\mathrm{1}} {dx} \\ $$$$=\lceil\left({a}+\mathrm{1}\right)\leftarrow{gamma}\:{function} \\ $$$$={a}! \\ $$$${dI}\left({a}\right)={a}!{da} \\ $$$${I}\left({a}\right)=\int\lceil\left({a}+\mathrm{1}\right){da} \\ $$
Commented by Dwaipayan Shikari last updated on 23/Oct/20
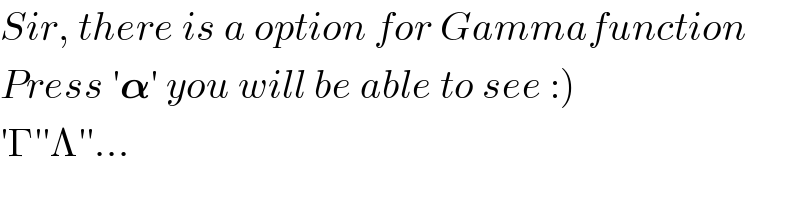
$${Sir},\:{there}\:{is}\:{a}\:{option}\:{for}\:{Gammafunction} \\ $$$$\left.{Press}\:'\boldsymbol{\alpha}'\:{you}\:{will}\:{be}\:{able}\:{to}\:{see}\::\right) \\ $$$$'\Gamma''\Lambda''... \\ $$
Commented by TANMAY PANACEA last updated on 23/Oct/20

$${ok}\:{thank}\:{you} \\ $$
Answered by Dwaipayan Shikari last updated on 23/Oct/20
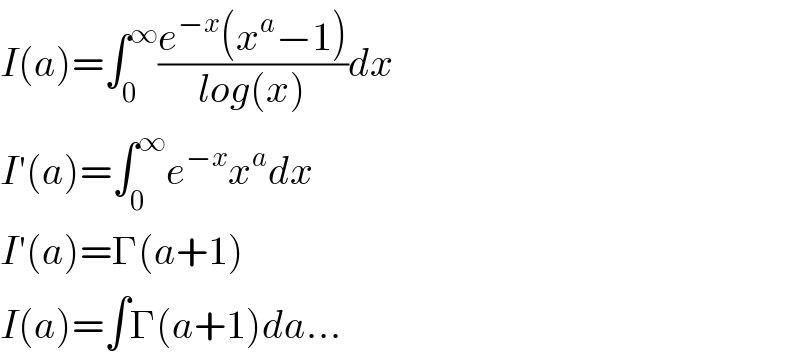
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} \left({x}^{{a}} −\mathrm{1}\right)}{{log}\left({x}\right)}{dx} \\ $$$${I}'\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {x}^{{a}} {dx} \\ $$$${I}'\left({a}\right)=\Gamma\left({a}+\mathrm{1}\right) \\ $$$${I}\left({a}\right)=\int\Gamma\left({a}+\mathrm{1}\right){da}... \\ $$
