Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 218583 by Nicholas666 last updated on 12/Apr/25

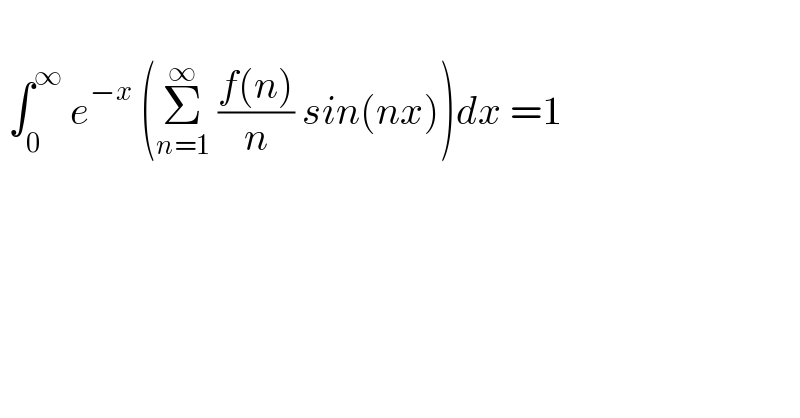
∫_(0 ) ^∞ e^(−x) (Σ_(n=1) ^∞ ((f(n))/n) sin(nx))dx =1

$$ \\ $$$$\:\int_{\mathrm{0}\:} ^{\infty} \:{e}^{−{x}} \:\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{f}\left({n}\right)}{{n}}\:{sin}\left({nx}\right)\right){dx}\:=\mathrm{1} \\ $$$$ \\ $$

Answered by aleks041103 last updated on 12/Apr/25

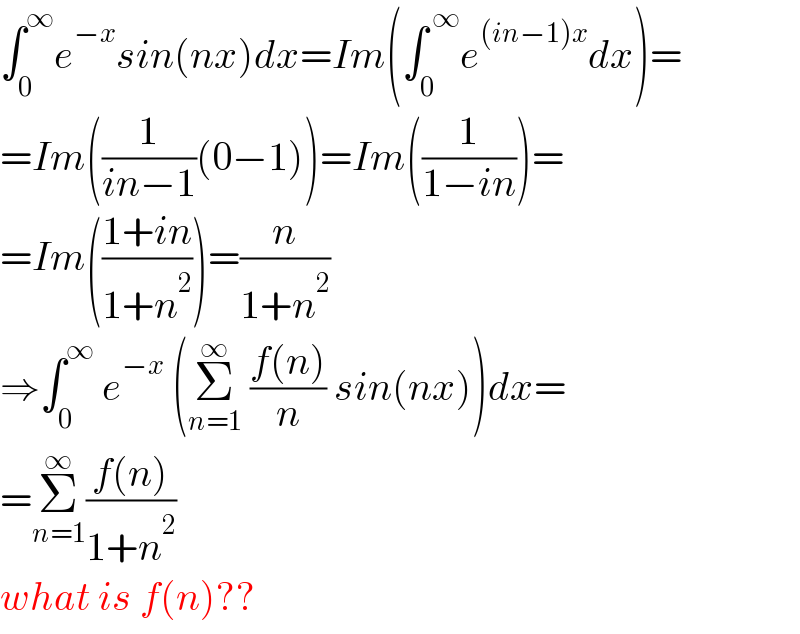
∫_0 ^∞ e^(−x) sin(nx)dx=Im(∫_0 ^( ∞) e^((in−1)x) dx)= =Im((1/(in−1))(0−1))=Im((1/(1−in)))= =Im(((1+in)/(1+n^2 )))=(n/(1+n^2 )) ⇒∫_(0 ) ^∞ e^(−x) (Σ_(n=1) ^∞ ((f(n))/n) sin(nx))dx= =Σ_(n=1) ^∞ ((f(n))/(1+n^2 )) what is f(n)??

$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {sin}\left({nx}\right){dx}={Im}\left(\int_{\mathrm{0}} ^{\:\infty} {e}^{\left({in}−\mathrm{1}\right){x}} {dx}\right)= \\ $$$$={Im}\left(\frac{\mathrm{1}}{{in}−\mathrm{1}}\left(\mathrm{0}−\mathrm{1}\right)\right)={Im}\left(\frac{\mathrm{1}}{\mathrm{1}−{in}}\right)= \\ $$$$={Im}\left(\frac{\mathrm{1}+{in}}{\mathrm{1}+{n}^{\mathrm{2}} }\right)=\frac{{n}}{\mathrm{1}+{n}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}\:} ^{\infty} \:{e}^{−{x}} \:\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{f}\left({n}\right)}{{n}}\:{sin}\left({nx}\right)\right){dx}= \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{f}\left({n}\right)}{\mathrm{1}+{n}^{\mathrm{2}} } \\ $$$${what}\:{is}\:{f}\left({n}\right)?? \\ $$

Commented by aleks041103 last updated on 12/Apr/25

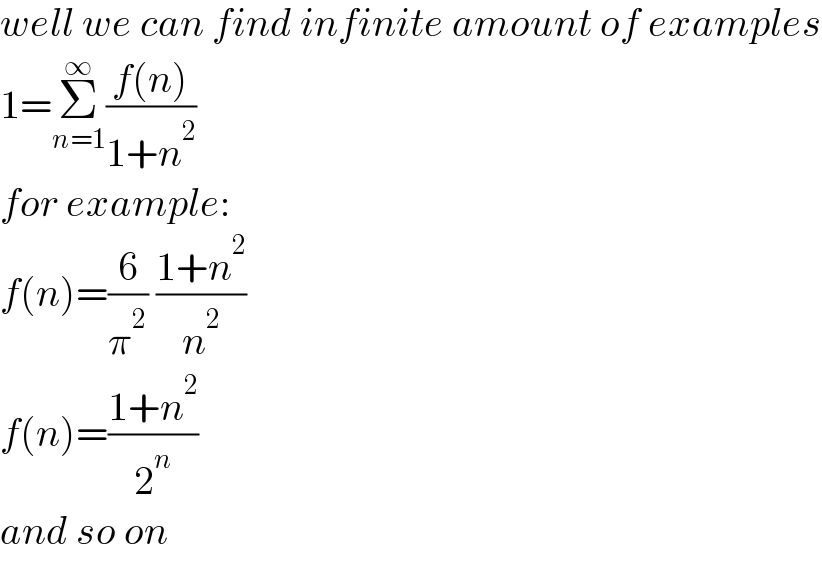
well we can find infinite amount of examples 1=Σ_(n=1) ^∞ ((f(n))/(1+n^2 )) for example: f(n)=(6/π^2 ) ((1+n^2 )/n^2 ) f(n)=((1+n^2 )/2^n ) and so on

$${well}\:{we}\:{can}\:{find}\:{infinite}\:{amount}\:{of}\:{examples} \\ $$$$\mathrm{1}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{f}\left({n}\right)}{\mathrm{1}+{n}^{\mathrm{2}} } \\ $$$${for}\:{example}: \\ $$$${f}\left({n}\right)=\frac{\mathrm{6}}{\pi^{\mathrm{2}} }\:\frac{\mathrm{1}+{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} } \\ $$$${f}\left({n}\right)=\frac{\mathrm{1}+{n}^{\mathrm{2}} }{\mathrm{2}^{{n}} } \\ $$$${and}\:{so}\:{on} \\ $$

Commented by Nicholas666 last updated on 12/Apr/25

asking to find a function f(n) wich, when expressed in a series and then integrated over the factor e^(−x) , yields the value 1

$$\mathrm{asking}\:\mathrm{to}\:\mathrm{find}\:\mathrm{a}\:\mathrm{function}\:{f}\left({n}\right)\:\mathrm{wich}, \\ $$$$\mathrm{when}\:\mathrm{expressed}\:\mathrm{in}\:\mathrm{a}\:\mathrm{series}\:\mathrm{and}\:\mathrm{then}\:\mathrm{integrated}\: \\ $$$$\mathrm{over}\:\mathrm{the}\:\mathrm{factor}\:{e}^{−{x}} ,\:\mathrm{yields}\:\mathrm{the}\:\mathrm{value}\:\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com