Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 189489 by mnjuly1970 last updated on 17/Mar/23

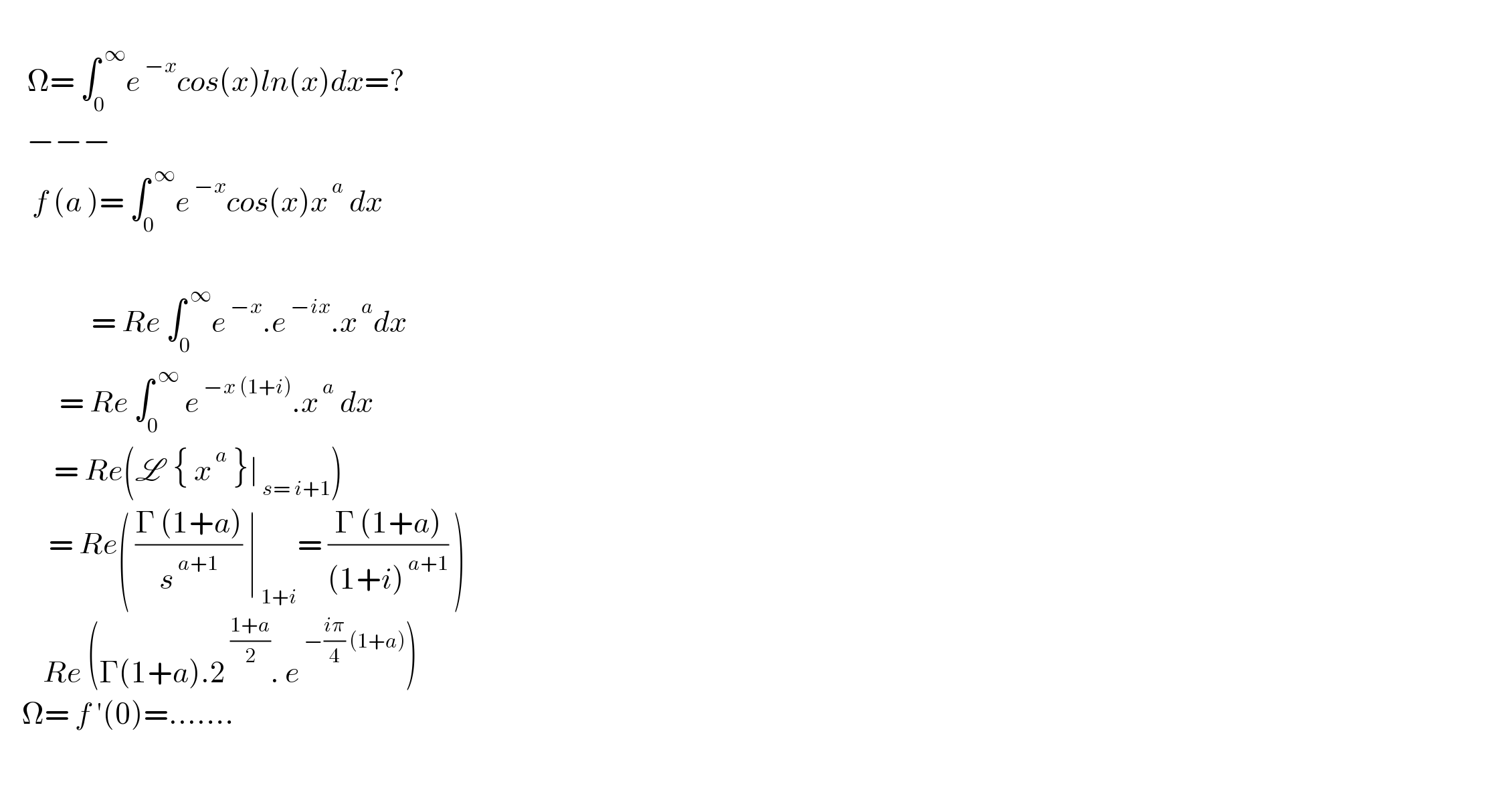
Ω= ∫_0 ^( ∞) e^( −x) cos(x)ln(x)dx=? −−− f (a )= ∫_0 ^( ∞) e^( −x) cos(x)x^( a) dx = Re ∫_0 ^( ∞) e^( −x) .e^( −ix) .x^( a) dx = Re ∫_0 ^( ∞) e^( −x (1+i)) .x^( a) dx = Re(L { x^( a) }∣_( s= i+1) ) = Re( ((Γ (1+a))/s^( a+1) ) ∣_( 1+i) = ((Γ (1+a))/((1+i)^( a+1) )) ) Re (Γ(1+a).2^( ((1+a)/2)) . e^( −((iπ)/4) (1+a)) ) Ω= f ′(0)=.......

$$ \\ $$$$\:\:\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{x}} {cos}\left({x}\right){ln}\left({x}\right){dx}=? \\ $$$$\:\:\:\:\:−−− \\ $$$$\:\:\:\:\:\:{f}\:\left({a}\:\right)=\:\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{x}} {cos}\left({x}\right){x}^{\:{a}} \:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{Re}\:\int_{\mathrm{0}} ^{\:\infty} {e}^{\:−{x}} .{e}^{\:−{ix}} .{x}^{\:{a}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:{Re}\:\int_{\mathrm{0}} ^{\:\infty} \:{e}^{\:−{x}\:\left(\mathrm{1}+{i}\right)} .{x}^{\:{a}} \:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:{Re}\left(\mathscr{L}\:\:\left\{\:{x}^{\:{a}} \:\right\}\mid_{\:{s}=\:{i}+\mathrm{1}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:=\:{Re}\left(\:\frac{\Gamma\:\left(\mathrm{1}+{a}\right)}{{s}^{\:{a}+\mathrm{1}} }\:\mid_{\:\mathrm{1}+{i}} =\:\frac{\Gamma\:\left(\mathrm{1}+{a}\right)}{\left(\mathrm{1}+{i}\right)^{\:{a}+\mathrm{1}} }\:\right) \\ $$$$\:\:\:\:\:\:\:\:{Re}\:\left(\Gamma\left(\mathrm{1}+{a}\right).\mathrm{2}^{\:\frac{\mathrm{1}+{a}}{\mathrm{2}}} .\:{e}^{\:−\frac{{i}\pi}{\mathrm{4}}\:\left(\mathrm{1}+{a}\right)} \right) \\ $$$$\:\:\:\:\Omega=\:{f}\:'\left(\mathrm{0}\right)=....... \\ $$$$\:\: \\ $$

Commented by Gbenga last updated on 19/Mar/23

here is my solution....... 𝛀=∫_0 ^∞ e^(−x) cos(x)ln(x)dx e^(−ix) =cos(x)+isin(x) Re(e^(−ix) )=cos(x) 𝛀=Re∫_0 ^∞ e^(−x) e^(−ix) ln(x)dx 𝛀=Re∫_0 ^∞ e^(−x(1+i)) ln(x)dx 𝛀=Re[(d/da)∫_0 ^∞ e^(−x(1+i)) x^a dx]_(a=0) let x(1+i)=u x=(u/(1+i )) dx=(du/(1+i)) 𝛀=Re[(d/da)[(1/((1+i)^(a+1) ))[∫_0 ^∞ e^(−u) u^a du]_(a=0) 𝛀=Re[(d/da)[((𝚪(a+1))/((1+i)^(a+1) ))]_(a=0) 𝛀=Re(−((𝚪(a+1))/((1+i)^(a+1) ))[−𝛙^0 (a+1)+log(1+i)])_(a=0) Re(−(1/((1+i)))[−𝛙^0 (1)+log(1+i)])=−(𝛄/2)+Re((−(1/2)+(i/2))log(1+i))=−(𝛄/2)−(𝛑/8)−((log(2))/4) ∴ our answer is −(𝛄/2)−(𝛑/8)−((log(2))/4) ★Small Laplace★

$$\boldsymbol{\mathrm{here}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{my}}\:\boldsymbol{\mathrm{solution}}....... \\ $$$$\boldsymbol{\Omega}=\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}} \\ $$$$\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{ix}}} =\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{isin}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\boldsymbol{\mathrm{R}{e}}\left(\boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{ix}}} \right)=\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\boldsymbol{\Omega}=\boldsymbol{\mathrm{R}{e}}\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{ix}}} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}} \\ $$$$\boldsymbol{\Omega}=\boldsymbol{\mathrm{Re}}\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)} \boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}} \\ $$$$\boldsymbol{\Omega}=\boldsymbol{\mathrm{R}{e}}\left[\frac{\boldsymbol{\mathrm{d}}}{\boldsymbol{\mathrm{da}}}\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{x}}\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)} \boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{a}}} \boldsymbol{\mathrm{dx}}\right]_{\boldsymbol{\mathrm{a}}=\mathrm{0}} \\ $$$$\boldsymbol{\mathrm{let}}\:\boldsymbol{\mathrm{x}}\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)=\boldsymbol{\mathrm{u}}\:\boldsymbol{\mathrm{x}}=\frac{\boldsymbol{\mathrm{u}}}{\mathrm{1}+\boldsymbol{\mathrm{i}}\:}\:\boldsymbol{\mathrm{dx}}=\frac{\boldsymbol{\mathrm{du}}}{\mathrm{1}+\boldsymbol{\mathrm{i}}} \\ $$$$\boldsymbol{\Omega}=\boldsymbol{\mathrm{Re}}\left[\frac{\boldsymbol{\mathrm{d}}}{\boldsymbol{\mathrm{da}}}\left[\frac{\mathrm{1}}{\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)^{\boldsymbol{\mathrm{a}}+\mathrm{1}} }\left[\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{e}}^{−\boldsymbol{\mathrm{u}}} \boldsymbol{\mathrm{u}}^{\boldsymbol{\mathrm{a}}} \boldsymbol{\mathrm{du}}\right]_{\boldsymbol{\mathrm{a}}=\mathrm{0}} \right.\right. \\ $$$$\boldsymbol{\Omega}=\boldsymbol{\mathrm{R}{e}}\left[\frac{\boldsymbol{\mathrm{d}}}{\boldsymbol{\mathrm{da}}}\left[\frac{\boldsymbol{\Gamma}\left(\boldsymbol{\mathrm{a}}+\mathrm{1}\right)}{\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)^{\boldsymbol{\mathrm{a}}+\mathrm{1}} }\right]_{\boldsymbol{\mathrm{a}}=\mathrm{0}} \right. \\ $$$$\boldsymbol{\Omega}=\boldsymbol{\mathrm{Re}}\left(−\frac{\boldsymbol{\Gamma}\left(\boldsymbol{\mathrm{a}}+\mathrm{1}\right)}{\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)^{\boldsymbol{\mathrm{a}}+\mathrm{1}} }\left[−\boldsymbol{\psi}^{\mathrm{0}} \left(\boldsymbol{\mathrm{a}}+\mathrm{1}\right)+\boldsymbol{\mathrm{log}}\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)\right]\right)_{\boldsymbol{\mathrm{a}}=\mathrm{0}} \\ $$$$\boldsymbol{\mathrm{Re}}\left(−\frac{\mathrm{1}}{\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)}\left[−\boldsymbol{\psi}^{\mathrm{0}} \left(\mathrm{1}\right)+\boldsymbol{\mathrm{log}}\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)\right]\right)=−\frac{\boldsymbol{\gamma}}{\mathrm{2}}+\boldsymbol{\mathrm{Re}}\left(\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\boldsymbol{\mathrm{i}}}{\mathrm{2}}\right)\boldsymbol{\mathrm{log}}\left(\mathrm{1}+\boldsymbol{\mathrm{i}}\right)\right)=−\frac{\boldsymbol{\gamma}}{\mathrm{2}}−\frac{\boldsymbol{\pi}}{\mathrm{8}}−\frac{\boldsymbol{\mathrm{log}}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\therefore\:\boldsymbol{\mathrm{our}}\:\boldsymbol{\mathrm{answer}}\:\boldsymbol{\mathrm{is}}\:−\frac{\boldsymbol{\gamma}}{\mathrm{2}}−\frac{\boldsymbol{\pi}}{\mathrm{8}}−\frac{\boldsymbol{\mathrm{log}}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\bigstar\boldsymbol{{Small}}\:\boldsymbol{{Laplace}}\bigstar \\ $$

Answered by leodera last updated on 17/May/23

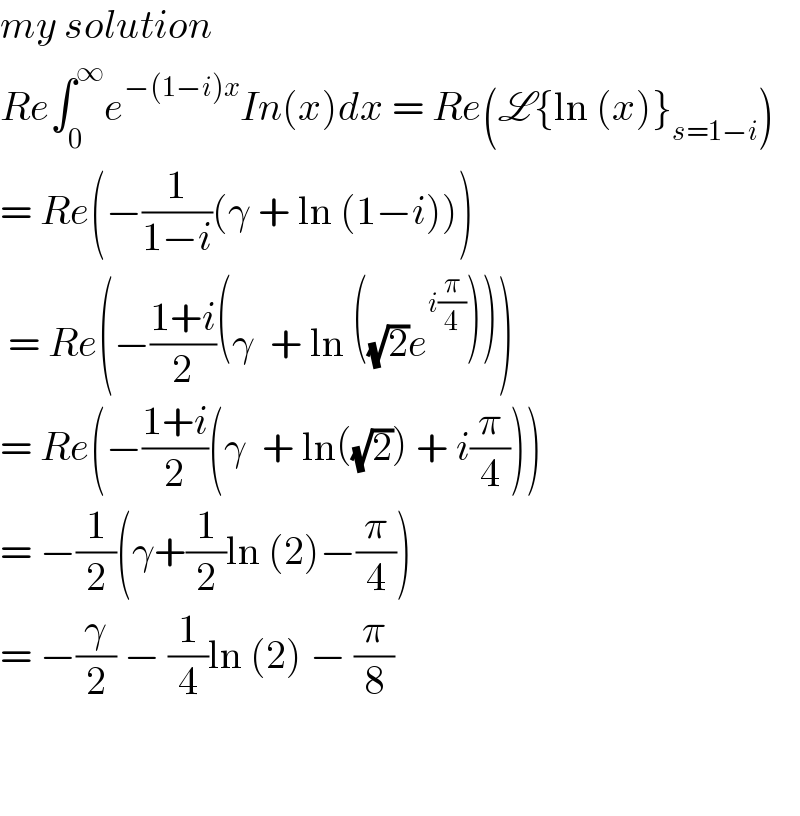
my solution Re∫_0 ^∞ e^(−(1−i)x) In(x)dx = Re(L{ln (x)}_(s=1−i) ) = Re(−(1/(1−i))(γ + ln (1−i))) = Re(−((1+i)/2)(γ + ln ((√2)e^(i(π/4)) ))) = Re(−((1+i)/2)(γ + ln((√2)) + i(π/4))) = −(1/2)(γ+(1/2)ln (2)−(π/4)) = −(γ/2) − (1/4)ln (2) − (π/8)

$${my}\:{solution} \\ $$$${Re}\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{1}−{i}\right){x}} {In}\left({x}\right){dx}\:=\:{Re}\left(\mathscr{L}\left\{\mathrm{ln}\:\left({x}\right)\right\}_{{s}=\mathrm{1}−{i}} \right) \\ $$$$=\:{Re}\left(−\frac{\mathrm{1}}{\mathrm{1}−{i}}\left(\gamma\:+\:\mathrm{ln}\:\left(\mathrm{1}−{i}\right)\right)\right) \\ $$$$\:=\:{Re}\left(−\frac{\mathrm{1}+{i}}{\mathrm{2}}\left(\gamma\:\:+\:\mathrm{ln}\:\left(\sqrt{\mathrm{2}}{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)\right)\right) \\ $$$$=\:{Re}\left(−\frac{\mathrm{1}+{i}}{\mathrm{2}}\left(\gamma\:\:+\:\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)\:+\:{i}\frac{\pi}{\mathrm{4}}\right)\right) \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\gamma+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{4}}\right) \\ $$$$=\:−\frac{\gamma}{\mathrm{2}}\:−\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}\right)\:−\:\frac{\pi}{\mathrm{8}}\: \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com