
Question Number 97465 by hosein_golmakani last updated on 08/Jun/20
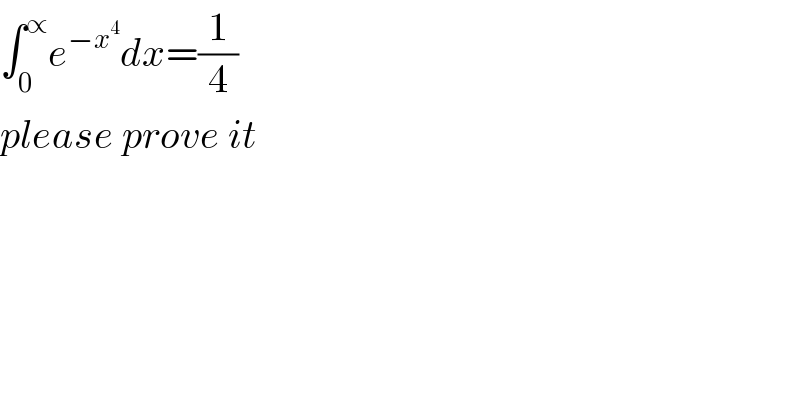
$$\int_{\mathrm{0}} ^{\propto} {e}^{−{x}^{\mathrm{4}} } {dx}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${please}\:{prove}\:{it} \\ $$
Commented by PRITHWISH SEN 2 last updated on 08/Jun/20
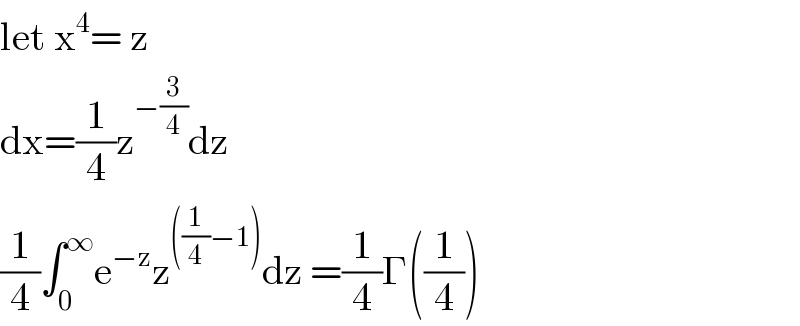
$$\mathrm{let}\:\mathrm{x}^{\mathrm{4}} =\:\mathrm{z} \\ $$$$\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{z}^{−\frac{\mathrm{3}}{\mathrm{4}}} \mathrm{dz}\:\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{z}} \mathrm{z}^{\left(\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}\right)} \mathrm{dz}\:=\frac{\mathrm{1}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\: \\ $$
Answered by smridha last updated on 08/Jun/20
![let x^2 =t so I=(1/2)∫_0 ^∞ e^(−t^2 ) t^(−(1/2)) dt =(1/4)[2∫_0 ^∞ e^(−t^2 ) t^(2(1/4)−1) dt] =(1/4)𝚪((1/4)) I think Ans is wrong..](Q97472.png)
$$\boldsymbol{{let}}\:\boldsymbol{{x}}^{\mathrm{2}} =\boldsymbol{{t}}\: \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \boldsymbol{{e}}^{−\boldsymbol{{t}}^{\mathrm{2}} } \boldsymbol{{t}}^{−\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{dt}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{2}\int_{\mathrm{0}} ^{\infty} \boldsymbol{{e}}^{−\boldsymbol{{t}}^{\mathrm{2}} } \boldsymbol{{t}}^{\mathrm{2}\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \boldsymbol{{dt}}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\boldsymbol{{I}}\:\boldsymbol{{think}}\:\boldsymbol{{Ans}}\:\boldsymbol{{is}}\:\boldsymbol{{wrong}}.. \\ $$
Answered by mathmax by abdo last updated on 08/Jun/20

$$\mathrm{error}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}\:...! \\ $$
