Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 206773 by MaruMaru last updated on 24/Apr/24

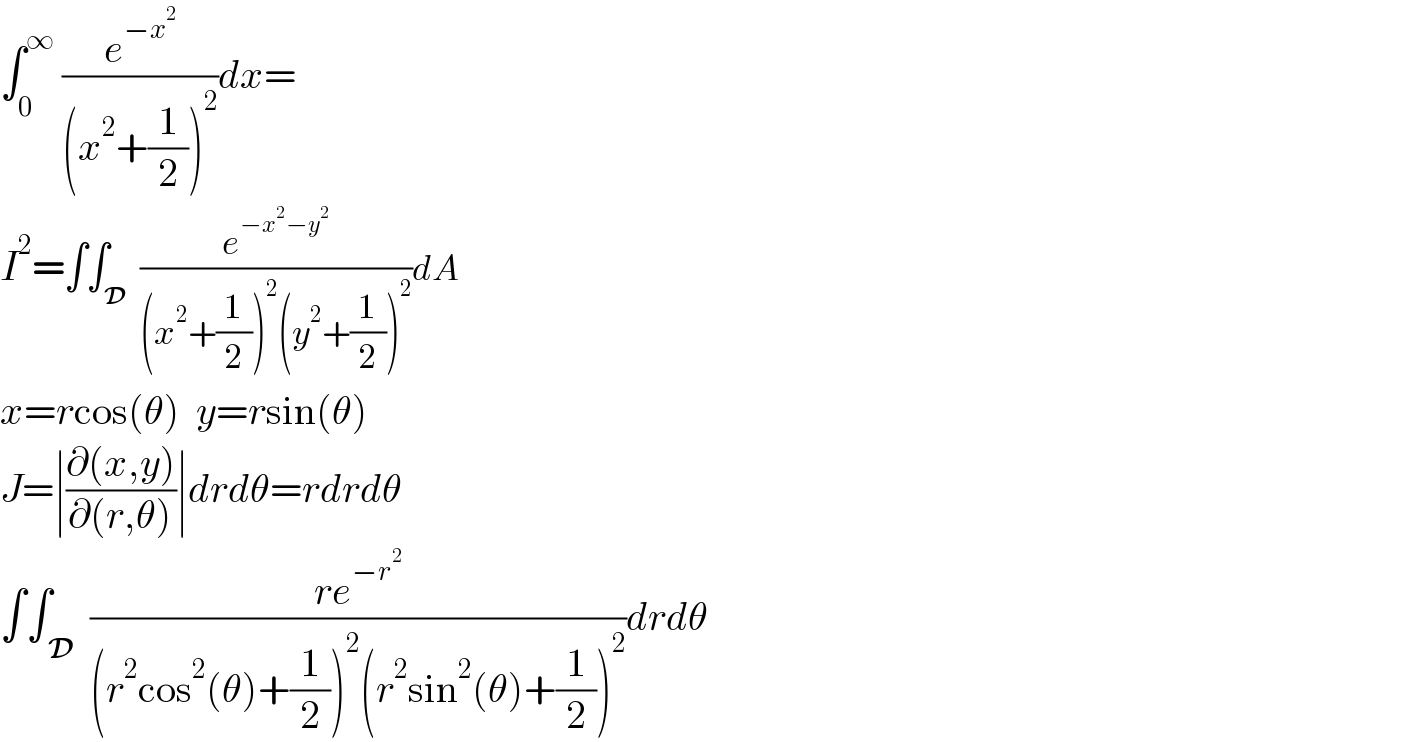
∫_0 ^∞ (e^(−x^2 ) /((x^2 +(1/2))^2 ))dx= I^2 =∫∫_( D) (e^(−x^2 −y^2 ) /((x^2 +(1/2))^2 (y^2 +(1/2))^2 ))dA x=rcos(θ) y=rsin(θ) J=∣((∂(x,y))/(∂(r,θ)))∣drdθ=rdrdθ ∫∫_( D) ((re^(−r^2 ) )/((r^2 cos^2 (θ)+(1/2))^2 (r^2 sin^2 (θ)+(1/2))^2 ))drdθ

$$\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}= \\ $$$${I}^{\mathrm{2}} =\int\int_{\:\boldsymbol{\mathcal{D}}} \:\frac{{e}^{−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \left({y}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dA} \\ $$$${x}={r}\mathrm{cos}\left(\theta\right)\:\:{y}={r}\mathrm{sin}\left(\theta\right) \\ $$$${J}=\mid\frac{\partial\left({x},{y}\right)}{\partial\left({r},\theta\right)}\mid{drd}\theta={rdrd}\theta \\ $$$$\int\int_{\:\boldsymbol{\mathcal{D}}} \:\frac{{re}^{−{r}^{\mathrm{2}} } }{\left({r}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \left(\theta\right)+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \left({r}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\theta\right)+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{drd}\theta \\ $$

Commented by MaruMaru last updated on 24/Apr/24

next...???

$${next}...??? \\ $$

Commented by Frix last updated on 24/Apr/24

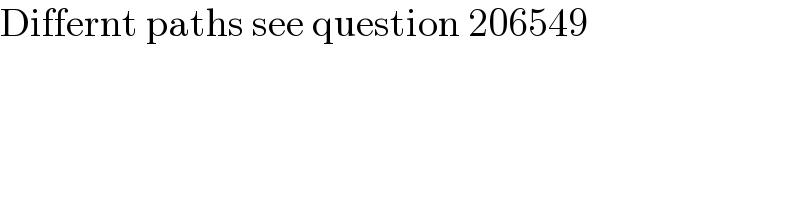
Differnt paths see question 206549

$$\mathrm{Differnt}\:\mathrm{paths}\:\mathrm{see}\:\mathrm{question}\:\mathrm{206549} \\ $$

Commented by MaruMaru last updated on 25/Apr/24

wow thx

$${wow}\:{thx} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com