
Question Number 206549 by Shrodinger last updated on 18/Apr/24
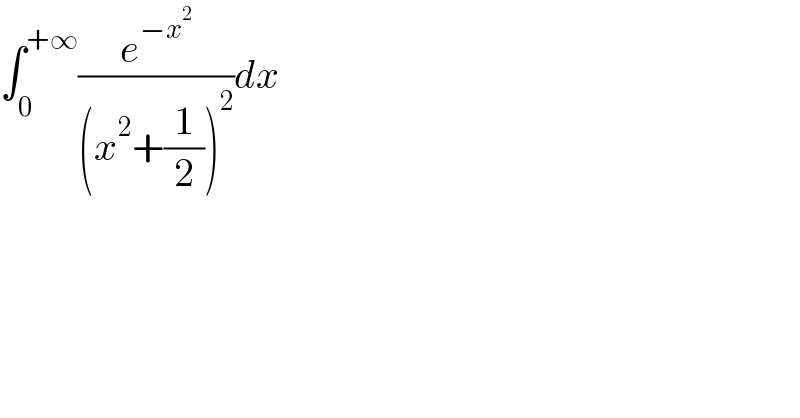
$$\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by Frix last updated on 18/Apr/24

$$\sqrt{\pi} \\ $$
Commented by Shrodinger last updated on 18/Apr/24

$${how}\:{please}\:? \\ $$
Answered by Frix last updated on 18/Apr/24
![∫_0 ^∞ (e^(−x^2 ) /((x^2 +(1/2))^2 ))dx=2∫_0 ^∞ e^(−x^2 ) (1−((x^4 +x^2 −(1/4))/((x^2 +(1/2))^2 )))dx= =2∫_0 ^∞ e^(−x^2 ) dx−2∫_0 ^∞ e^(−x^2 ) ((x^4 +x^2 −(1/4))/((x^2 +(1/2))^2 ))dx 2∫_0 ^∞ e^(−x^2 ) dx=(√π) −2∫_0 ^∞ e^(−x^2 ) ((x^4 +x^2 −(1/4))/((x^2 +(1/2))^2 ))dx=[((xe^(−x^2 ) )/(x^2 +(1/2)))]_0 ^∞ =0](Q206567.png)
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}=\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−{x}^{\mathrm{2}} } \left(\mathrm{1}−\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\right){dx}= \\ $$$$=\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−{x}^{\mathrm{2}} } {dx}−\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−{x}^{\mathrm{2}} } \frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx} \\ $$$$\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−{x}^{\mathrm{2}} } {dx}=\sqrt{\pi} \\ $$$$−\mathrm{2}\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{e}^{−{x}^{\mathrm{2}} } \frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}=\left[\frac{{x}\mathrm{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}}\right]_{\mathrm{0}} ^{\infty} =\mathrm{0} \\ $$
Answered by Berbere last updated on 18/Apr/24
![∫_0 ^∞ (e^(−tx^2 ) /(x^2 +a))dx=f(t);f(0)=∫_0 ^∞ (dx/(x^2 +a))=(1/( (√a))).(π/2) f′(t)=∫_0 ^∞ ((−x^2 )/(x^2 +a))e^(−tx^2 ) dx=−∫_0 ^∞ e^(−tx^2 ) dx+af(t) f′(t)=−(1/2)(√(π/t))+af(t) f(t)=ke^(at) ⇒k′=−(1/2)(√(π/t))e^(−at) .⇒k=−(√π)∫(e^(−at) /(2 (√t)))dt;t=x^2 =−(√π)∫e^(−ax^2 ) dx=^(y=x(√a)) −(π/( 2)).(1/( (√a)))erf(x(√a))=−(√((2π)/a))erf((√(at)))+c f(t)=(−(π/( 2(√a)))erf((√(at)))+(π/(2(√a))))e^(at) =(π/(2(√a)))(1−erf((√(at))))e^(at) =(π/(2(√a)))erfc((√(at)))e^(at) (∂f/∂a)=−∫_0 ^∞ (1/((x^2 +a)^2 ))e^(−tx^2 ) ∣_((t=1,a=(1/2))) =−A −(∂f/∂a)(1,(1/2))=−(∂/∂a)(π/(2(√a)))erfc((√a))e^a ∣_(a=(1/2)) =−[−(π/(4a(√a)))erfc((√a))e^a +(π/(2(√a)))(−(1/( (√(aπ))))e^(−a) e^a +erfc((√a))e^a ).] (π/(2(√(1/2))))erfc((√(1/2)))−(π/( (√2)))(−((√2)/( (√π)))+erc((1/( (√2))))e^(1/2) )=(√π) ∫_0 ^∞ (e^(−x^2 ) /((x^2 +(1/2))^2 ))=(√π)](Q206574.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{tx}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +{a}}{dx}={f}\left({t}\right);{f}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{2}} +{a}}=\frac{\mathrm{1}}{\:\sqrt{{a}}}.\frac{\pi}{\mathrm{2}} \\ $$$${f}'\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \frac{−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{a}}{e}^{−{tx}^{\mathrm{2}} } {dx}=−\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}^{\mathrm{2}} } {dx}+{af}\left({t}\right) \\ $$$${f}'\left({t}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\pi}{{t}}}+{af}\left({t}\right) \\ $$$${f}\left({t}\right)={ke}^{{at}} \Rightarrow{k}'=−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\pi}{{t}}}{e}^{−{at}} .\Rightarrow{k}=−\sqrt{\pi}\int\frac{{e}^{−{at}} }{\mathrm{2}\:\sqrt{{t}}}{dt};{t}={x}^{\mathrm{2}} \\ $$$$=−\sqrt{\pi}\int{e}^{−{ax}^{\mathrm{2}} } {dx}\overset{{y}={x}\sqrt{{a}}} {=}−\frac{\pi}{\:\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{{a}}}{erf}\left({x}\sqrt{{a}}\right)=−\sqrt{\frac{\mathrm{2}\pi}{{a}}}{erf}\left(\sqrt{{at}}\right)+{c} \\ $$$${f}\left({t}\right)=\left(−\frac{\pi}{\:\mathrm{2}\sqrt{{a}}}{erf}\left(\sqrt{{at}}\right)+\frac{\pi}{\mathrm{2}\sqrt{{a}}}\right){e}^{{at}} =\frac{\pi}{\mathrm{2}\sqrt{{a}}}\left(\mathrm{1}−{erf}\left(\sqrt{{at}}\right)\right){e}^{{at}} \\ $$$$=\frac{\pi}{\mathrm{2}\sqrt{{a}}}{erfc}\left(\sqrt{{at}}\right){e}^{{at}} \\ $$$$\frac{\partial{f}}{\partial{a}}=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +{a}\right)^{\mathrm{2}} }{e}^{−{tx}^{\mathrm{2}} } \mid_{\left({t}=\mathrm{1},{a}=\frac{\mathrm{1}}{\mathrm{2}}\right)} =−{A} \\ $$$$−\frac{\partial{f}}{\partial{a}}\left(\mathrm{1},\frac{\mathrm{1}}{\mathrm{2}}\right)=−\frac{\partial}{\partial{a}}\frac{\pi}{\mathrm{2}\sqrt{{a}}}{erfc}\left(\sqrt{{a}}\right){e}^{{a}} \mid_{{a}=\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=−\left[−\frac{\pi}{\mathrm{4}{a}\sqrt{{a}}}{erfc}\left(\sqrt{{a}}\right){e}^{{a}} +\frac{\pi}{\mathrm{2}\sqrt{{a}}}\left(−\frac{\mathrm{1}}{\:\sqrt{{a}\pi}}{e}^{−{a}} {e}^{{a}} +{erfc}\left(\sqrt{{a}}\right){e}^{{a}} \right).\right] \\ $$$$\frac{\pi}{\mathrm{2}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}}{erfc}\left(\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}\right)−\frac{\pi}{\:\sqrt{\mathrm{2}}}\left(−\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\pi}}+{erc}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right){e}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)=\sqrt{\pi} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\pi} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
