Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 219793 by SdC355 last updated on 02/May/25

∫_0 ^( ∞) (e^(−t) /(t^2 +1)) dt=?

$$\int_{\mathrm{0}} ^{\:\infty} \:\:\frac{{e}^{−{t}} }{{t}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{d}{t}=? \\ $$

Answered by breniam last updated on 03/May/25

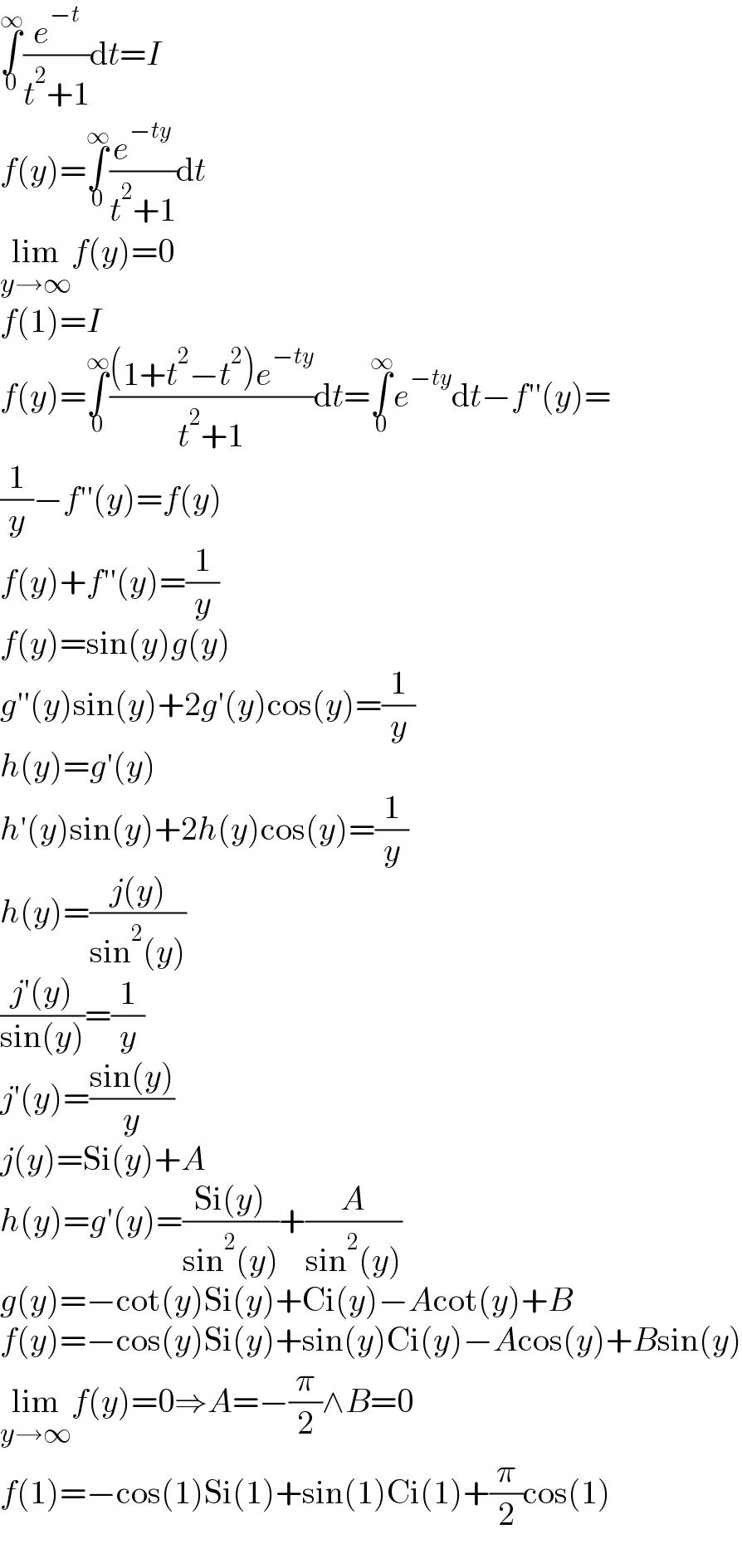
∫_0 ^∞ (e^(−t) /(t^2 +1))dt=I f(y)=∫_0 ^∞ (e^(−ty) /(t^2 +1))dt lim_(y→∞) f(y)=0 f(1)=I f(y)=∫_0 ^∞ (((1+t^2 −t^2 )e^(−ty) )/(t^2 +1))dt=∫_0 ^∞ e^(−ty) dt−f′′(y)= (1/y)−f′′(y)=f(y) f(y)+f′′(y)=(1/y) f(y)=sin(y)g(y) g′′(y)sin(y)+2g′(y)cos(y)=(1/y) h(y)=g′(y) h′(y)sin(y)+2h(y)cos(y)=(1/y) h(y)=((j(y))/(sin^2 (y))) ((j′(y))/(sin(y)))=(1/y) j′(y)=((sin(y))/y) j(y)=Si(y)+A h(y)=g′(y)=((Si(y))/(sin^2 (y)))+(A/(sin^2 (y))) g(y)=−cot(y)Si(y)+Ci(y)−Acot(y)+B f(y)=−cos(y)Si(y)+sin(y)Ci(y)−Acos(y)+Bsin(y) lim_(y→∞) f(y)=0⇒A=−(π/2)∧B=0 f(1)=−cos(1)Si(1)+sin(1)Ci(1)+(π/2)cos(1)

$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{e}^{−{t}} }{{t}^{\mathrm{2}} +\mathrm{1}}\mathrm{d}{t}={I} \\ $$$${f}\left({y}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{e}^{−{ty}} }{{t}^{\mathrm{2}} +\mathrm{1}}\mathrm{d}{t} \\ $$$$\underset{{y}\rightarrow\infty} {\mathrm{lim}}{f}\left({y}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)={I} \\ $$$${f}\left({y}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} −{t}^{\mathrm{2}} \right){e}^{−{ty}} }{{t}^{\mathrm{2}} +\mathrm{1}}\mathrm{d}{t}=\underset{\mathrm{0}} {\overset{\infty} {\int}}{e}^{−{ty}} \mathrm{d}{t}−{f}''\left({y}\right)= \\ $$$$\frac{\mathrm{1}}{{y}}−{f}''\left({y}\right)={f}\left({y}\right) \\ $$$${f}\left({y}\right)+{f}''\left({y}\right)=\frac{\mathrm{1}}{{y}} \\ $$$${f}\left({y}\right)=\mathrm{sin}\left({y}\right){g}\left({y}\right) \\ $$$${g}''\left({y}\right)\mathrm{sin}\left({y}\right)+\mathrm{2}{g}'\left({y}\right)\mathrm{cos}\left({y}\right)=\frac{\mathrm{1}}{{y}} \\ $$$${h}\left({y}\right)={g}'\left({y}\right) \\ $$$${h}'\left({y}\right)\mathrm{sin}\left({y}\right)+\mathrm{2}{h}\left({y}\right)\mathrm{cos}\left({y}\right)=\frac{\mathrm{1}}{{y}} \\ $$$${h}\left({y}\right)=\frac{{j}\left({y}\right)}{\mathrm{sin}^{\mathrm{2}} \left({y}\right)} \\ $$$$\frac{{j}'\left({y}\right)}{\mathrm{sin}\left({y}\right)}=\frac{\mathrm{1}}{{y}} \\ $$$${j}'\left({y}\right)=\frac{\mathrm{sin}\left({y}\right)}{{y}} \\ $$$${j}\left({y}\right)=\mathrm{Si}\left({y}\right)+{A} \\ $$$${h}\left({y}\right)={g}'\left({y}\right)=\frac{\mathrm{Si}\left({y}\right)}{\mathrm{sin}^{\mathrm{2}} \left({y}\right)}+\frac{{A}}{\mathrm{sin}^{\mathrm{2}} \left({y}\right)} \\ $$$${g}\left({y}\right)=−\mathrm{cot}\left({y}\right)\mathrm{Si}\left({y}\right)+\mathrm{Ci}\left({y}\right)−{A}\mathrm{cot}\left({y}\right)+{B} \\ $$$${f}\left({y}\right)=−\mathrm{cos}\left({y}\right)\mathrm{Si}\left({y}\right)+\mathrm{sin}\left({y}\right)\mathrm{Ci}\left({y}\right)−{A}\mathrm{cos}\left({y}\right)+{B}\mathrm{sin}\left({y}\right) \\ $$$$\underset{{y}\rightarrow\infty} {\mathrm{lim}}{f}\left({y}\right)=\mathrm{0}\Rightarrow{A}=−\frac{\pi}{\mathrm{2}}\wedge{B}=\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)=−\mathrm{cos}\left(\mathrm{1}\right)\mathrm{Si}\left(\mathrm{1}\right)+\mathrm{sin}\left(\mathrm{1}\right)\mathrm{Ci}\left(\mathrm{1}\right)+\frac{\pi}{\mathrm{2}}\mathrm{cos}\left(\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com