
Question Number 6775 by Tawakalitu. last updated on 24/Jul/16
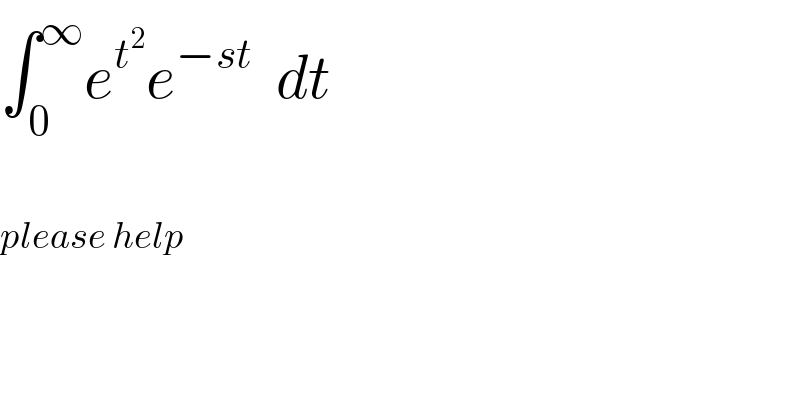
$$\int_{\mathrm{0}} ^{\infty} {e}^{{t}^{\mathrm{2}} } {e}^{−{st}} \:\:{dt} \\ $$$$ \\ $$$${please}\:{help} \\ $$
Answered by Yozzii last updated on 24/Jul/16

$${b}=\int_{\mathrm{0}} ^{\infty} {e}^{{t}^{\mathrm{2}} −{st}} {dt}=\int_{\mathrm{0}} ^{\infty} {e}^{\left({t}−\mathrm{0}.\mathrm{5}{s}\right)^{\mathrm{2}} −\mathrm{0}.\mathrm{25}{s}^{\mathrm{2}} } {dt} \\ $$$${b}={e}^{−\mathrm{0}.\mathrm{25}{s}^{\mathrm{2}} } \int_{\mathrm{0}} ^{\infty} {e}^{\left({t}−\mathrm{0}.\mathrm{5}{s}\right)^{\mathrm{2}} } {dt}. \\ $$$${u}={t}−\mathrm{0}.\mathrm{5}{s}\Rightarrow{du}={dt} \\ $$$$\therefore{b}={e}^{−\mathrm{0}.\mathrm{25}{s}^{\mathrm{2}} } \left(\int_{−\mathrm{0}.\mathrm{5}{s}} ^{\mathrm{0}} {e}^{{u}^{\mathrm{2}} } {du}+\int_{\mathrm{0}} ^{\infty} {e}^{{u}^{\mathrm{2}} } {du}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{{u}^{\mathrm{2}} } {du}\:{is}\:{divergent}\:{while}\:\int_{−\mathrm{0}.\mathrm{5}{s}} ^{\mathrm{0}} {e}^{{u}^{\mathrm{2}} } {du} \\ $$$${is}\:{finite}. \\ $$$$\therefore\:{For}\:{nonzero}\:{s}\in\mathbb{R},\:{b}={e}^{−\mathrm{0}.\mathrm{25}{s}^{\mathrm{2}} } \left\{\int_{−\mathrm{0}.\mathrm{5}{s}} ^{\mathrm{0}} {e}^{{u}^{\mathrm{2}} } {du}+\int_{\mathrm{0}} ^{\infty} {e}^{{u}^{\mathrm{2}} } {du}\right\} \\ $$$${does}\:{not}\:{exist}.\: \\ $$$${If}\:{s}=\mathrm{0},{b}=\int_{\mathrm{0}} ^{\infty} {e}^{{t}^{\mathrm{2}} } {dt}\:{which}\:{is}\:{divergent}\:{also}. \\ $$
Commented by Tawakalitu. last updated on 24/Jul/16
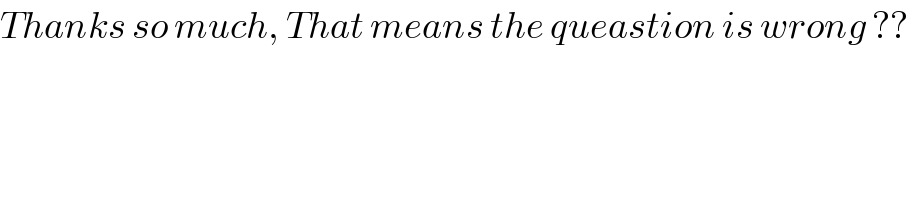
$${Thanks}\:{so}\:{much},\:{That}\:{means}\:{the}\:{queastion}\:{is}\:{wrong}\:?? \\ $$
Commented by Yozzii last updated on 24/Jul/16
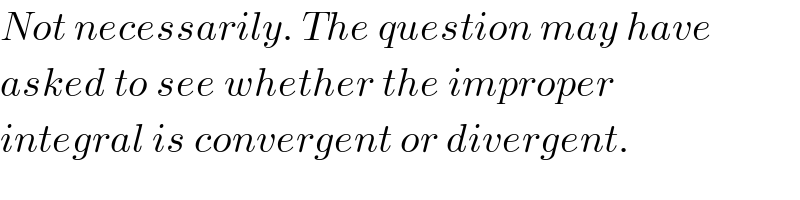
$${Not}\:{necessarily}.\:{The}\:{question}\:{may}\:{have} \\ $$$${asked}\:{to}\:{see}\:{whether}\:{the}\:{improper} \\ $$$${integral}\:{is}\:{convergent}\:{or}\:{divergent}. \\ $$
Commented by Tawakalitu. last updated on 24/Jul/16

$${Thanks} \\ $$
Commented by Tawakalitu. last updated on 25/Jul/16
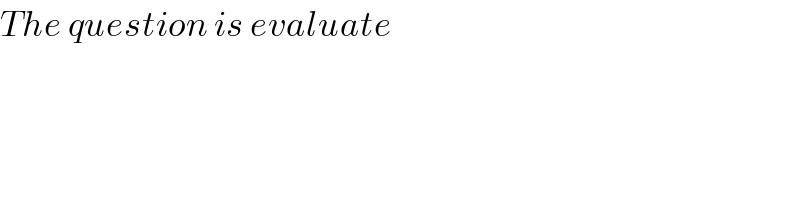
$${The}\:{question}\:{is}\:{evaluate} \\ $$
