Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 101828 by floor(10²Eta[1]) last updated on 05/Jul/20

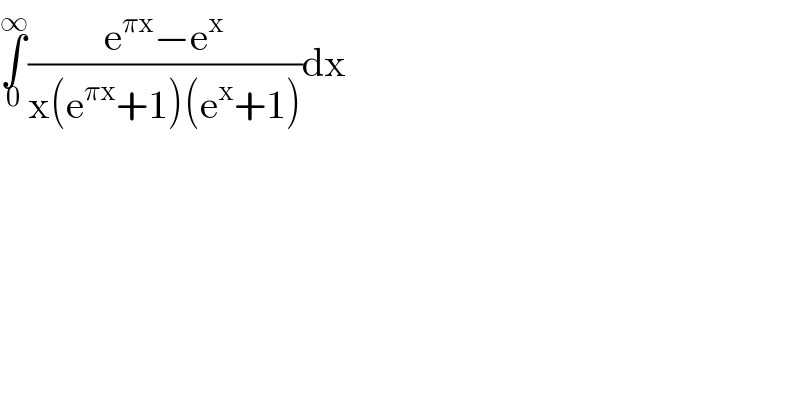
∫_0 ^∞ ((e^(πx) −e^x )/(x(e^(πx) +1)(e^x +1)))dx

$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{e}^{\pi\mathrm{x}} −\mathrm{e}^{\mathrm{x}} }{\mathrm{x}\left(\mathrm{e}^{\pi\mathrm{x}} +\mathrm{1}\right)\left(\mathrm{e}^{\mathrm{x}} +\mathrm{1}\right)}\mathrm{dx} \\ $$

Answered by maths mind last updated on 05/Jul/20

=∫_0 ^(+∞) (1/x){(1/((e^x +1)))−(1/(e^(πx) +1))}dx let f bee lik t≥0 well defind C_∞ f(t)=∫_0 ^(+∞) (1/x){(1/(e^x +1))−(1/(e^(πx) +1))}e^(−xt) dx f′(t)=∫_0 ^(+∞) −(e^(−xt) /(e^x +1))dx+∫_0 ^(+∞) (e^(−xt) /(e^(πx) +1))dx =−∫_0 ^∞ e^(−x(t+1)) Σ_(k≥0) (−e^(−x) )^k dx+∫_0 ^(+∞) e^(−(t+π)) Σ(−e^(−πx) )^k dx =Σ_(k≥0) (−1)^(k+1) .(1/(k+t+1))+Σ_(k≥0) (((−1)^k )/(πk+t+π)) =Σ_(k≥0) ((((−1)^k )/(k+t+π))−(((−1)^k )/(k+t+1))) =Σ_(k≥0) ((1/(2k+t+π))−(1/(2k+t+1)))+Σ_(k≥0) ((1/(2k+2+t))−(1/(2k+t+π+1))) (1/(t+π))−(1/(t+1))+(1/(2+t))−(1/(t+π+1))+Σ_(k≥1) (−(1/(2k))+(1/(2k+t+π))+(1/(2k))−(1/(2k+t+1))) +Σ_(k≥1) ((1/(2k+2+t))−(1/(2k))+(1/(2k))−(1/(2k+t+π+1))) we have H(z)=Σ_(k≥1) ((1/k)−(1/(k+z)))^� ∀z∈C−{Z_− } we get f′(t)=(1/(t+π))−(1/(t+1))+(1/(t+2))−(1/(t+π+1))−(1/2)H(((t+π)/2))+(1/2)H(((t+1)/2)) −(1/2)H(((t+2)/2))+(1/2)H(((t+π+1)/2)) H(z)=Ψ(z+1)+γ we get f′(t)=(1/(t+π))−(1/(t+1))+(1/(t+2))−(1/(t+π+1))+(1/2)(Ψ(((t+3)/2))−Ψ(((t+π+2)/2))+Ψ(((t+π+1)/2))−Ψ(((t+2)/2))) f(t)=ln(((t+π)/(t+π+1)))+ln(((t+2)/(t+1)))+log(((Γ(((t+3)/2)))/(Γ(((t+2)/2)))))+log(((Γ(((t+π+1)/2)))/(Γ(((t+π+2)/2)))))+c wr used∫Ψ(z)dz=log(Γ(z))+c lim_(t→∞) f(t)=0 we need too finde thislim_(x→∞) ((Γ(x+(1/2)))/(Γ(x))) Γ(z+a)∼(√(2πz)).z^(z+a−(1/2)) e^(−z) f(t)→0 f(0)=∫_0 ^(+∞) ((e^(πx) −e^x )/(x(e^x +1)(e^(πx) +1)))dx=ln((π/(π+1)))+ln(2)+log(((Γ((3/2))Γ(((π+1)/2)))/(Γ(1)Γ(((π+2)/2)))))

$$=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{{x}}\left\{\frac{\mathrm{1}}{\left({e}^{{x}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{{e}^{\pi{x}} +\mathrm{1}}\right\}{dx} \\ $$$${let}\:{f}\:{bee}\:{lik}\:{t}\geqslant\mathrm{0}\:{well}\:{defind}\:{C}_{\infty} \\ $$$${f}\left({t}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{{x}}\left\{\frac{\mathrm{1}}{{e}^{{x}} +\mathrm{1}}−\frac{\mathrm{1}}{{e}^{\pi{x}} +\mathrm{1}}\right\}{e}^{−{xt}} {dx} \\ $$$${f}'\left({t}\right)=\int_{\mathrm{0}} ^{+\infty} −\frac{{e}^{−{xt}} }{{e}^{{x}} +\mathrm{1}}{dx}+\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{xt}} }{{e}^{\pi{x}} +\mathrm{1}}{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} {e}^{−{x}\left({t}+\mathrm{1}\right)} \underset{{k}\geqslant\mathrm{0}} {\sum}\left(−{e}^{−{x}} \right)^{{k}} {dx}+\int_{\mathrm{0}} ^{+\infty} {e}^{−\left({t}+\pi\right)} \Sigma\left(−{e}^{−\pi{x}} \right)^{{k}} {dx} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} .\frac{\mathrm{1}}{{k}+{t}+\mathrm{1}}+\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\pi{k}+{t}+\pi} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\left(\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+{t}+\pi}−\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+{t}+\mathrm{1}}\right) \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{2}{k}+{t}+\pi}−\frac{\mathrm{1}}{\mathrm{2}{k}+{t}+\mathrm{1}}\right)+\underset{{k}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{2}+{t}}−\frac{\mathrm{1}}{\mathrm{2}{k}+{t}+\pi+\mathrm{1}}\right) \\ $$$$\frac{\mathrm{1}}{{t}+\pi}−\frac{\mathrm{1}}{{t}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}+{t}}−\frac{\mathrm{1}}{{t}+\pi+\mathrm{1}}+\underset{{k}\geqslant\mathrm{1}} {\sum}\left(−\frac{\mathrm{1}}{\mathrm{2}{k}}+\frac{\mathrm{1}}{\mathrm{2}{k}+{t}+\pi}+\frac{\mathrm{1}}{\mathrm{2}{k}}−\frac{\mathrm{1}}{\mathrm{2}{k}+{t}+\mathrm{1}}\right) \\ $$$$+\underset{{k}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{2}+{t}}−\frac{\mathrm{1}}{\mathrm{2}{k}}+\frac{\mathrm{1}}{\mathrm{2}{k}}−\frac{\mathrm{1}}{\mathrm{2}{k}+{t}+\pi+\mathrm{1}}\right) \\ $$$${we}\:{have}\:{H}\left({z}\right)=\underset{{k}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+{z}}\bar {\right)}\forall{z}\in\mathbb{C}−\left\{\mathbb{Z}_{−} \right\} \\ $$$${we}\:{get}\:{f}'\left({t}\right)=\frac{\mathrm{1}}{{t}+\pi}−\frac{\mathrm{1}}{{t}+\mathrm{1}}+\frac{\mathrm{1}}{{t}+\mathrm{2}}−\frac{\mathrm{1}}{{t}+\pi+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}{H}\left(\frac{{t}+\pi}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{H}\left(\frac{{t}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{H}\left(\frac{{t}+\mathrm{2}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{H}\left(\frac{{t}+\pi+\mathrm{1}}{\mathrm{2}}\right) \\ $$$${H}\left({z}\right)=\Psi\left({z}+\mathrm{1}\right)+\gamma \\ $$$${we}\:{get} \\ $$$${f}'\left({t}\right)=\frac{\mathrm{1}}{{t}+\pi}−\frac{\mathrm{1}}{{t}+\mathrm{1}}+\frac{\mathrm{1}}{{t}+\mathrm{2}}−\frac{\mathrm{1}}{{t}+\pi+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\left(\Psi\left(\frac{{t}+\mathrm{3}}{\mathrm{2}}\right)−\Psi\left(\frac{{t}+\pi+\mathrm{2}}{\mathrm{2}}\right)+\Psi\left(\frac{{t}+\pi+\mathrm{1}}{\mathrm{2}}\right)−\Psi\left(\frac{{t}+\mathrm{2}}{\mathrm{2}}\right)\right) \\ $$$${f}\left({t}\right)={ln}\left(\frac{{t}+\pi}{{t}+\pi+\mathrm{1}}\right)+{ln}\left(\frac{{t}+\mathrm{2}}{{t}+\mathrm{1}}\right)+{log}\left(\frac{\Gamma\left(\frac{{t}+\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{t}+\mathrm{2}}{\mathrm{2}}\right)}\right)+{log}\left(\frac{\Gamma\left(\frac{{t}+\pi+\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{t}+\pi+\mathrm{2}}{\mathrm{2}}\right)}\right)+{c} \\ $$$${wr}\:{used}\int\Psi\left({z}\right){dz}={log}\left(\Gamma\left({z}\right)\right)+{c} \\ $$$$\underset{{t}\rightarrow\infty} {\mathrm{lim}}{f}\left({t}\right)=\mathrm{0} \\ $$$${we}\:{need}\:{too}\:{finde}\:{this}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\Gamma\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({x}\right)} \\ $$$$\Gamma\left({z}+{a}\right)\sim\sqrt{\mathrm{2}\pi{z}}.{z}^{{z}+{a}−\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{z}} \\ $$$${f}\left({t}\right)\rightarrow\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{\pi{x}} −{e}^{{x}} }{{x}\left({e}^{{x}} +\mathrm{1}\right)\left({e}^{\pi{x}} +\mathrm{1}\right)}{dx}={ln}\left(\frac{\pi}{\pi+\mathrm{1}}\right)+{ln}\left(\mathrm{2}\right)+{log}\left(\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\pi+\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{1}\right)\Gamma\left(\frac{\pi+\mathrm{2}}{\mathrm{2}}\right)}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by floor(10²Eta[1]) last updated on 05/Jul/20

someone help me with the solution: I(t)=∫_0 ^∞ ((e^(tx) −e^x )/(x(e^(tx) +1)(e^x +1)))dx now i′m gonna derivate and integrate again: I′(t)=∫_0 ^∞ (∂/∂t)(((e^(tx) −e^x )/(x(e^(tx) +1)(e^x +1))))dx =∫_0 ^∞ (e^(tx) /((e^(tx) +1)^2 ))dx, u=e^(tx) +1⇒(du/t)=e^(tx) dx =(1/t)∫_2 ^∞ (du/u^2 )=(1/(2t)) ⇒I′(t)=(1/(2t))⇒I(t)=∫(1/(2t))=(1/2)ln∣t∣+C I(1)=0=C⇒I(t)=(1/2)ln∣t∣ ⇒I(π)=ln((√π))

$$\mathrm{someone}\:\mathrm{help}\:\mathrm{me}\:\mathrm{with}\:\mathrm{the}\:\mathrm{solution}: \\ $$$$\mathrm{I}\left(\mathrm{t}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{e}^{\mathrm{tx}} −\mathrm{e}^{\mathrm{x}} }{\mathrm{x}\left(\mathrm{e}^{\mathrm{tx}} +\mathrm{1}\right)\left(\mathrm{e}^{\mathrm{x}} +\mathrm{1}\right)}\mathrm{dx} \\ $$$$\mathrm{now}\:\mathrm{i}'\mathrm{m}\:\mathrm{gonna}\:\mathrm{derivate}\:\mathrm{and}\:\mathrm{integrate}\:\mathrm{again}: \\ $$$$\mathrm{I}'\left(\mathrm{t}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\partial}{\partial\mathrm{t}}\left(\frac{\mathrm{e}^{\mathrm{tx}} −\mathrm{e}^{\mathrm{x}} }{\mathrm{x}\left(\mathrm{e}^{\mathrm{tx}} +\mathrm{1}\right)\left(\mathrm{e}^{\mathrm{x}} +\mathrm{1}\right)}\right)\mathrm{dx} \\ $$$$=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{e}^{\mathrm{tx}} }{\left(\mathrm{e}^{\mathrm{tx}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx},\:\mathrm{u}=\mathrm{e}^{\mathrm{tx}} +\mathrm{1}\Rightarrow\frac{\mathrm{du}}{\mathrm{t}}=\mathrm{e}^{\mathrm{tx}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{t}}\underset{\mathrm{2}} {\overset{\infty} {\int}}\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2t}} \\ $$$$\Rightarrow\mathrm{I}'\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{2t}}\Rightarrow\mathrm{I}\left(\mathrm{t}\right)=\int\frac{\mathrm{1}}{\mathrm{2t}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{t}\mid+\mathrm{C} \\ $$$$\mathrm{I}\left(\mathrm{1}\right)=\mathrm{0}=\mathrm{C}\Rightarrow\mathrm{I}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{t}\mid \\ $$$$\Rightarrow\mathrm{I}\left(\pi\right)=\mathrm{ln}\left(\sqrt{\pi}\right) \\ $$

Answered by mathmax by abdo last updated on 05/Jul/20

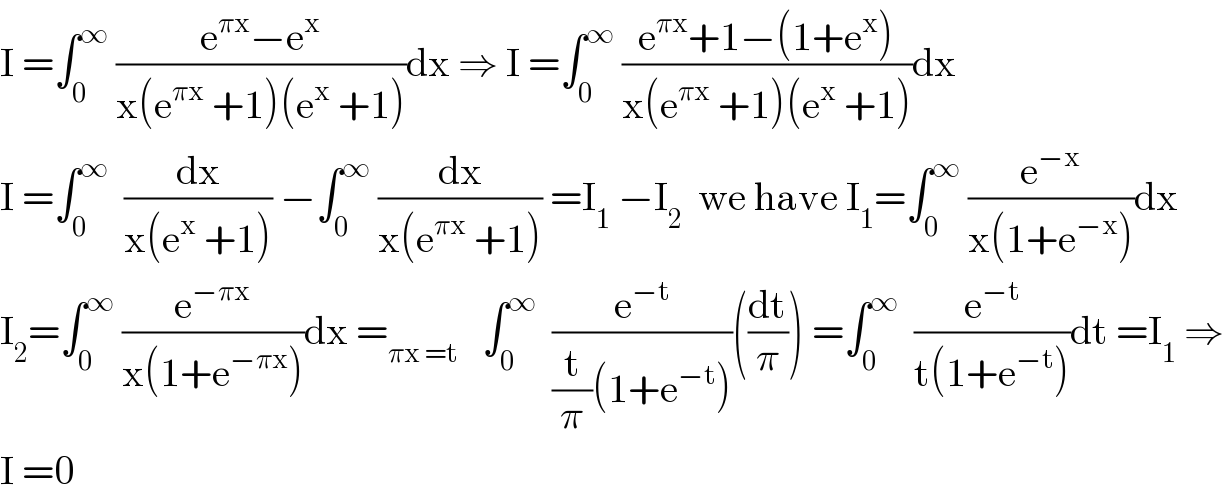
I =∫_0 ^∞ ((e^(πx) −e^x )/(x(e^(πx) +1)(e^x +1)))dx ⇒ I =∫_0 ^∞ ((e^(πx) +1−(1+e^x ))/(x(e^(πx) +1)(e^x +1)))dx I =∫_0 ^∞ (dx/(x(e^x +1))) −∫_0 ^∞ (dx/(x(e^(πx) +1))) =I_1 −I_2 we have I_1 =∫_0 ^∞ (e^(−x) /(x(1+e^(−x) )))dx I_2 =∫_0 ^∞ (e^(−πx) /(x(1+e^(−πx) )))dx =_(πx =t) ∫_0 ^∞ (e^(−t) /((t/π)(1+e^(−t) )))((dt/π)) =∫_0 ^∞ (e^(−t) /(t(1+e^(−t) )))dt =I_1 ⇒ I =0

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\pi\mathrm{x}} −\mathrm{e}^{\mathrm{x}} }{\mathrm{x}\left(\mathrm{e}^{\pi\mathrm{x}} \:+\mathrm{1}\right)\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}\right)}\mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\pi\mathrm{x}} +\mathrm{1}−\left(\mathrm{1}+\mathrm{e}^{\mathrm{x}} \right)}{\mathrm{x}\left(\mathrm{e}^{\pi\mathrm{x}} \:+\mathrm{1}\right)\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}\right)}\mathrm{dx} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{e}^{\mathrm{x}} \:+\mathrm{1}\right)}\:−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{e}^{\pi\mathrm{x}} \:+\mathrm{1}\right)}\:=\mathrm{I}_{\mathrm{1}} \:−\mathrm{I}_{\mathrm{2}} \:\:\mathrm{we}\:\mathrm{have}\:\mathrm{I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{x}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{x}} \right)}\mathrm{dx} \\ $$$$\mathrm{I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\pi\mathrm{x}} }{\mathrm{x}\left(\mathrm{1}+\mathrm{e}^{−\pi\mathrm{x}} \right)}\mathrm{dx}\:=_{\pi\mathrm{x}\:=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{t}} }{\frac{\mathrm{t}}{\pi}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{t}} \right)}\left(\frac{\mathrm{dt}}{\pi}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{t}} }{\mathrm{t}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{t}} \right)}\mathrm{dt}\:=\mathrm{I}_{\mathrm{1}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{0} \\ $$

Commented by maths mind last updated on 05/Jul/20

I_(1,) I_2 didnt cv

$$\:{I}_{\mathrm{1},} {I}_{\mathrm{2}} \:{didnt}\:\:{cv}\: \\ $$

Commented by mathmax by abdo last updated on 05/Jul/20

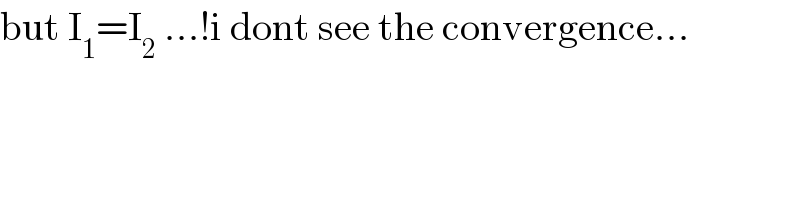
but I_1 =I_2 ...!i dont see the convergence...

$$\mathrm{but}\:\mathrm{I}_{\mathrm{1}} =\mathrm{I}_{\mathrm{2}} \:...!\mathrm{i}\:\mathrm{dont}\:\mathrm{see}\:\mathrm{the}\:\mathrm{convergence}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com