
Question Number 100557 by Mikael_786 last updated on 27/Jun/20
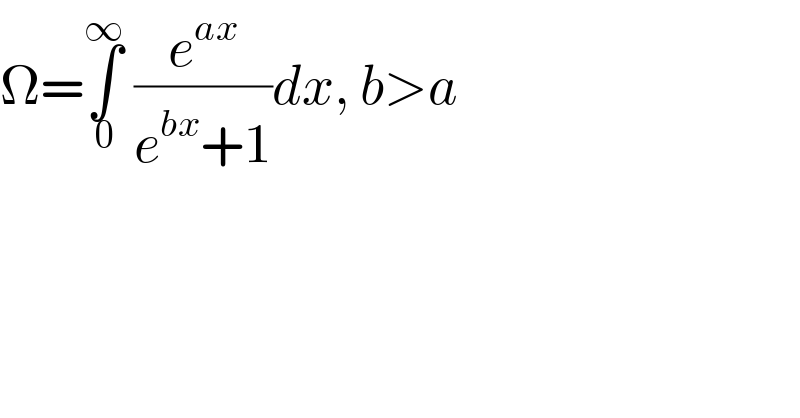
$$\Omega=\underset{\mathrm{0}} {\overset{\infty} {\int}}\:\frac{{e}^{{ax}} }{{e}^{{bx}} +\mathrm{1}}{dx},\:{b}>{a} \\ $$
Answered by mathmax by abdo last updated on 27/Jun/20
![Ω =∫_0 ^∞ (e^(ax) /(e^(bx) +1))dx⇒Ω =∫_0 ^∞ (e^((a−b)x) /(1+e^(−bx) ))dx =∫_0 ^∞ e^(−(b−a)x) Σ_(n=0) ^∞ (−1)^n e^(−nbx) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ e^(−(b−a+nb)x) dx =Σ_(n=0) ^∞ (−1)^n [((−1)/(b−a+nb)) e^(−(b−a+nb)x) ]_0 ^∞ =Σ_(n=0) ^∞ (((−1)^n )/(b−a +nb)) ....be continued....](Q100569.png)
$$\Omega\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\mathrm{ax}} }{\mathrm{e}^{\mathrm{bx}} \:+\mathrm{1}}\mathrm{dx}\Rightarrow\Omega\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{\left(\mathrm{a}−\mathrm{b}\right)\mathrm{x}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{bx}} }\mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{b}−\mathrm{a}\right)\mathrm{x}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{nbx}} \:\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{b}−\mathrm{a}+\mathrm{nb}\right)\mathrm{x}} \:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\left[\frac{−\mathrm{1}}{\mathrm{b}−\mathrm{a}+\mathrm{nb}}\:\mathrm{e}^{−\left(\mathrm{b}−\mathrm{a}+\mathrm{nb}\right)\mathrm{x}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{b}−\mathrm{a}\:+\mathrm{nb}}\:\:....\mathrm{be}\:\mathrm{continued}.... \\ $$
Answered by mathmax by abdo last updated on 27/Jun/20
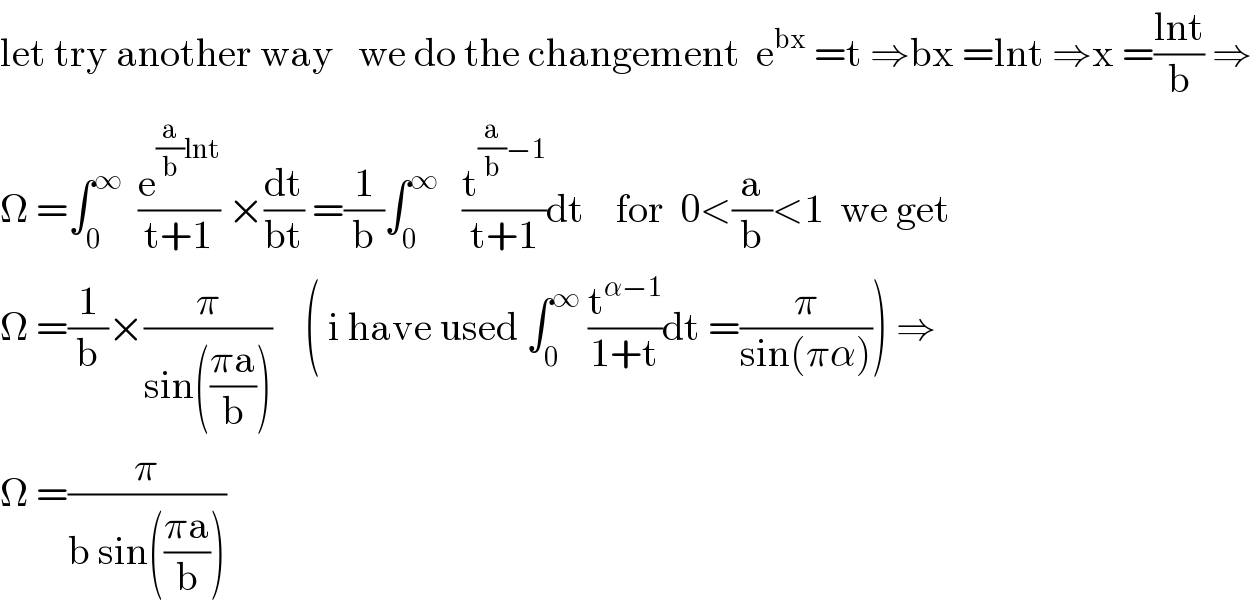
$$\mathrm{let}\:\mathrm{try}\:\mathrm{another}\:\mathrm{way}\:\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\:\mathrm{e}^{\mathrm{bx}} \:=\mathrm{t}\:\Rightarrow\mathrm{bx}\:=\mathrm{lnt}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{lnt}}{\mathrm{b}}\:\Rightarrow \\ $$$$\Omega\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{\frac{\mathrm{a}}{\mathrm{b}}\mathrm{lnt}} }{\mathrm{t}+\mathrm{1}}\:×\frac{\mathrm{dt}}{\mathrm{bt}}\:=\frac{\mathrm{1}}{\mathrm{b}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{t}^{\frac{\mathrm{a}}{\mathrm{b}}−\mathrm{1}} }{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:\:\:\:\mathrm{for}\:\:\mathrm{0}<\frac{\mathrm{a}}{\mathrm{b}}<\mathrm{1}\:\:\mathrm{we}\:\mathrm{get}\:\: \\ $$$$\Omega\:=\frac{\mathrm{1}}{\mathrm{b}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi\mathrm{a}}{\mathrm{b}}\right)}\:\:\:\:\left(\:\mathrm{i}\:\mathrm{have}\:\mathrm{used}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\alpha−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\pi}{\mathrm{sin}\left(\pi\alpha\right)}\right)\:\Rightarrow \\ $$$$\Omega\:=\frac{\pi}{\mathrm{b}\:\mathrm{sin}\left(\frac{\pi\mathrm{a}}{\mathrm{b}}\right)} \\ $$
Commented by Mikael_786 last updated on 28/Jun/20

$${thank}\:{you} \\ $$
