
Question Number 126183 by bobhans last updated on 18/Dec/20
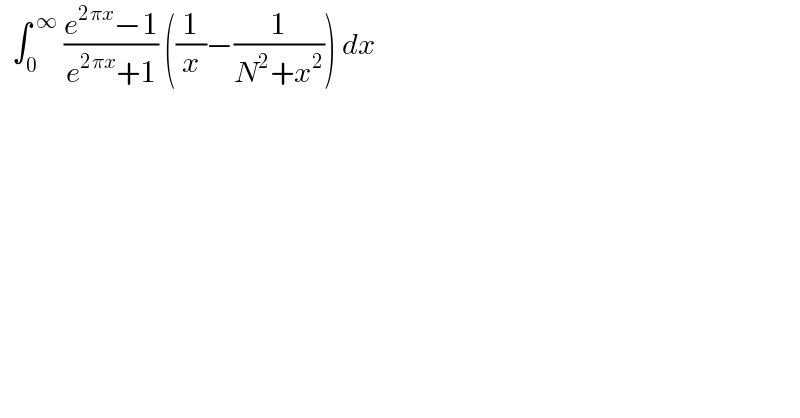
$$\:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}{{e}^{\mathrm{2}\pi{x}} +\mathrm{1}}\:\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{N}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right)\:{dx} \\ $$
Answered by Olaf last updated on 19/Dec/20
![Ω = ∫_0 ^∞ tanh(πx)[(1/x)−(1/(N^2 +x^2 ))]dx but tanh(πx)[(1/x)−(1/(N^2 +x^2 ))] ∼_∞ (1/x)−(1/(N^2 +x^2 )) and ∫_0 ^∞ ((1/x)−(1/(N^2 +x^2 )))dx diverges so I suppose Ω diverges...](Q126311.png)
$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \mathrm{tanh}\left(\pi{x}\right)\left[\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{N}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right]{dx} \\ $$$$\mathrm{but}\:\mathrm{tanh}\left(\pi{x}\right)\left[\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{N}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right]\:\underset{\infty} {\sim}\:\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{N}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{N}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right){dx}\:\mathrm{diverges} \\ $$$$\mathrm{so}\:\mathrm{I}\:\mathrm{suppose}\:\Omega\:\mathrm{diverges}... \\ $$
