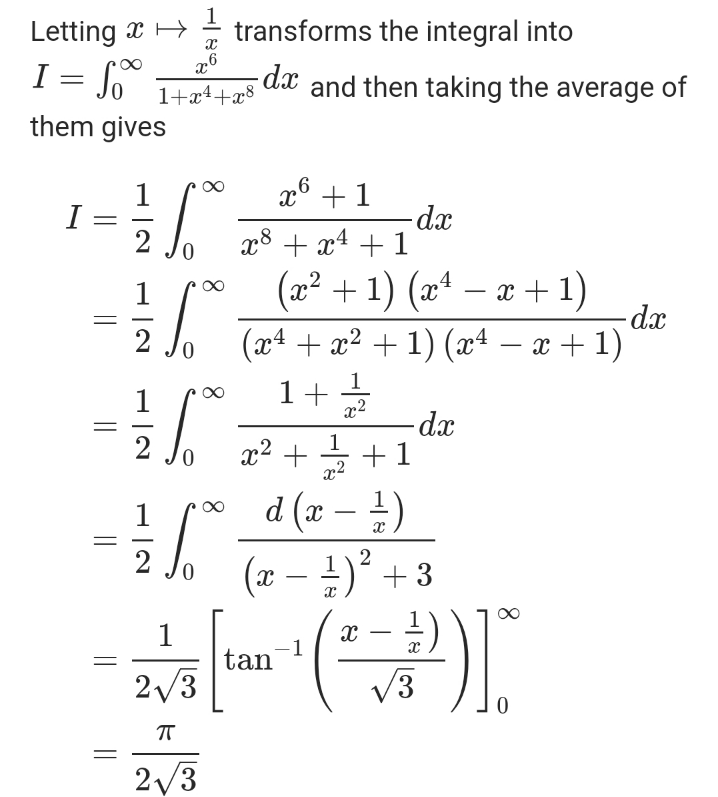Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 183977 by cortano1 last updated on 01/Jan/23

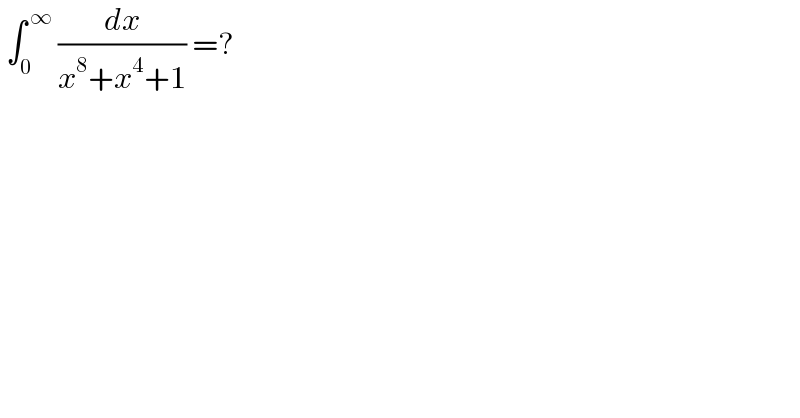
∫_0 ^( ∞) (dx/(x^8 +x^4 +1)) =?

$$\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{dx}}{{x}^{\mathrm{8}} +{x}^{\mathrm{4}} +\mathrm{1}}\:=?\: \\ $$

Answered by ARUNG_Brandon_MBU last updated on 01/Jan/23

Ω=∫_0 ^∞ (dx/(x^8 +x^4 +1))=∫_0 ^∞ ((1−x^4 )/(1−x^(12) ))dx=∫_0 ^1 ((1−x^4 )/(1−x^(12) ))dx+∫_1 ^∞ ((1−x^4 )/(1−x^(12) ))dx =∫_0 ^1 ((1−x^4 )/(1−x^(12) ))dx+∫_0 ^1 ((1−(1/x^4 ))/(1−(1/x^(12) )))∙(1/x^2 )dx=∫_0 ^1 ((1−x^4 )/(1−x^(12) ))dx+∫_0 ^1 ((x^(10) −x^6 )/(x^(12) −1))dx =∫_0 ^1 ((1−x^4 +x^6 −x^(10) )/(1−x^(12) ))dx=(1/(12))∫_0 ^1 ((x^(−((11)/(12))) −x^(−(7/(12))) +x^(−(5/(12))) −x^(−(1/(12))) )/(1−x))dx =(1/(12))(ψ(((11)/(12)))−ψ((1/(12)))+ψ((5/(12)))−ψ((7/(12))))=(1/(12))(πcot((π/(12)))−πcot(((5π)/(12)))) =(π/(12))((((√6)+(√2))/( (√6)−(√2)))−(((√6)−(√2))/( (√6)+(√2))))=(π/(12))((((8+4(√3))−(8−4(√3)))/4))=((π(√3))/6)

$$\Omega=\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{8}} +{x}^{\mathrm{4}} +\mathrm{1}}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{x}^{\mathrm{4}} }{\mathrm{1}−{x}^{\mathrm{12}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{4}} }{\mathrm{1}−{x}^{\mathrm{12}} }{dx}+\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}−{x}^{\mathrm{4}} }{\mathrm{1}−{x}^{\mathrm{12}} }{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{4}} }{\mathrm{1}−{x}^{\mathrm{12}} }{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{12}} }}\centerdot\frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{4}} }{\mathrm{1}−{x}^{\mathrm{12}} }{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{10}} −{x}^{\mathrm{6}} }{{x}^{\mathrm{12}} −\mathrm{1}}{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{4}} +{x}^{\mathrm{6}} −{x}^{\mathrm{10}} }{\mathrm{1}−{x}^{\mathrm{12}} }{dx}=\frac{\mathrm{1}}{\mathrm{12}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{−\frac{\mathrm{11}}{\mathrm{12}}} −{x}^{−\frac{\mathrm{7}}{\mathrm{12}}} +{x}^{−\frac{\mathrm{5}}{\mathrm{12}}} −{x}^{−\frac{\mathrm{1}}{\mathrm{12}}} }{\mathrm{1}−{x}}{dx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{12}}\left(\psi\left(\frac{\mathrm{11}}{\mathrm{12}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{12}}\right)+\psi\left(\frac{\mathrm{5}}{\mathrm{12}}\right)−\psi\left(\frac{\mathrm{7}}{\mathrm{12}}\right)\right)=\frac{\mathrm{1}}{\mathrm{12}}\left(\pi\mathrm{cot}\left(\frac{\pi}{\mathrm{12}}\right)−\pi\mathrm{cot}\left(\frac{\mathrm{5}\pi}{\mathrm{12}}\right)\right) \\ $$$$\:\:\:\:=\frac{\pi}{\mathrm{12}}\left(\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}−\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}\right)=\frac{\pi}{\mathrm{12}}\left(\frac{\left(\mathrm{8}+\mathrm{4}\sqrt{\mathrm{3}}\right)−\left(\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}\right)}{\mathrm{4}}\right)=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$

Commented by MJS_new last updated on 01/Jan/23

great! happy new year!

$$\mathrm{great}! \\ $$$$\mathrm{happy}\:\mathrm{new}\:\mathrm{year}! \\ $$

Commented by Ar Brandon last updated on 01/Jan/23

Thank you, Sir �� Happy New Year ����

Answered by Ar Brandon last updated on 01/Jan/23

x^8 +x^4 +1=(x^4 +1)^2 −x^4 =(x^4 −x^2 +1)(x^4 +x^2 +1) I=∫(dx/(x^8 +x^4 +1))=∫(dx/((x^4 −x^2 +1)(x^4 +x^2 +1))) =(1/2)∫(((x^6 +1)−(x^6 −1))/((x^4 −x^2 +1)(x^4 +x^2 +1)))dx =(1/2)∫((x^2 +1)/(x^4 +x^2 +1))dx−(1/2)∫((x^2 −1)/(x^4 −x^2 +1))dx =(1/2)∫((1+(1/x^2 ))/(x^2 +1+(1/x^2 )))dx−(1/2)∫((1−(1/x^2 ))/(x^2 −1+(1/x^2 )))dx =(1/2)∫((1+(1/x^2 ))/((x−(1/x))^2 +3))dx−(1/2)∫((1−(1/x^2 ))/((x+(1/x))^2 −3))dx =(1/(2(√3)))arctan(((x^2 −1)/( (√3)x)))+(1/(2(√3)))argcoth(((x^2 +1)/( (√3)x)))+C =(1/(2(√3)))arctan(((x^2 −1)/( (√3)x)))+(1/(4(√3)))ln∣((x^2 +(√3)x+1)/(x^2 −(√3)x+1))∣+C ∫_0 ^∞ (dx/(x^8 +x^4 +1))=[(1/(2(√3)))arctan(((x^2 −1)/( (√3)x)))+(1/(4(√3)))ln∣((x^2 +(√3)x+1)/(x^2 −(√3)x+1))∣]_0 ^∞ ⇒ determinant (((∫_0 ^∞ (dx/(x^8 +x^4 +1))=(π/(2(√3))))))

$${x}^{\mathrm{8}} +{x}^{\mathrm{4}} +\mathrm{1}=\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} −{x}^{\mathrm{4}} =\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${I}=\int\frac{{dx}}{{x}^{\mathrm{8}} +{x}^{\mathrm{4}} +\mathrm{1}}=\int\frac{{dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left({x}^{\mathrm{6}} +\mathrm{1}\right)−\left({x}^{\mathrm{6}} −\mathrm{1}\right)}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}\right)}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} −\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{3}}{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{3}}{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{argcoth}\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{\mathrm{3}}{x}}\right)+{C} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{3}}{x}}\right)+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\mid+{C} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{8}} +{x}^{\mathrm{4}} +\mathrm{1}}=\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\:\sqrt{\mathrm{3}}{x}}\right)+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:\:\Rightarrow\begin{array}{|c|}{\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{8}} +{x}^{\mathrm{4}} +\mathrm{1}}=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}}\\\hline\end{array} \\ $$

Answered by universe last updated on 01/Jan/23

Terms of Service

Privacy Policy

Contact: info@tinkutara.com