
Question Number 117437 by frc2crc last updated on 11/Oct/20

$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{a}^{\mathrm{3}} +{x}^{\mathrm{3}} } \\ $$$$ \\ $$$${generaly} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{p}+{x}^{{n}} } \\ $$
Answered by AbduraufKodiriy last updated on 11/Oct/20

Commented by AbduraufKodiriy last updated on 11/Oct/20
$$\boldsymbol{{Sorry}}\:\boldsymbol{{for}}\:\boldsymbol{{my}}\:\boldsymbol{{mistakes}} \\ $$
Answered by Bird last updated on 12/Oct/20
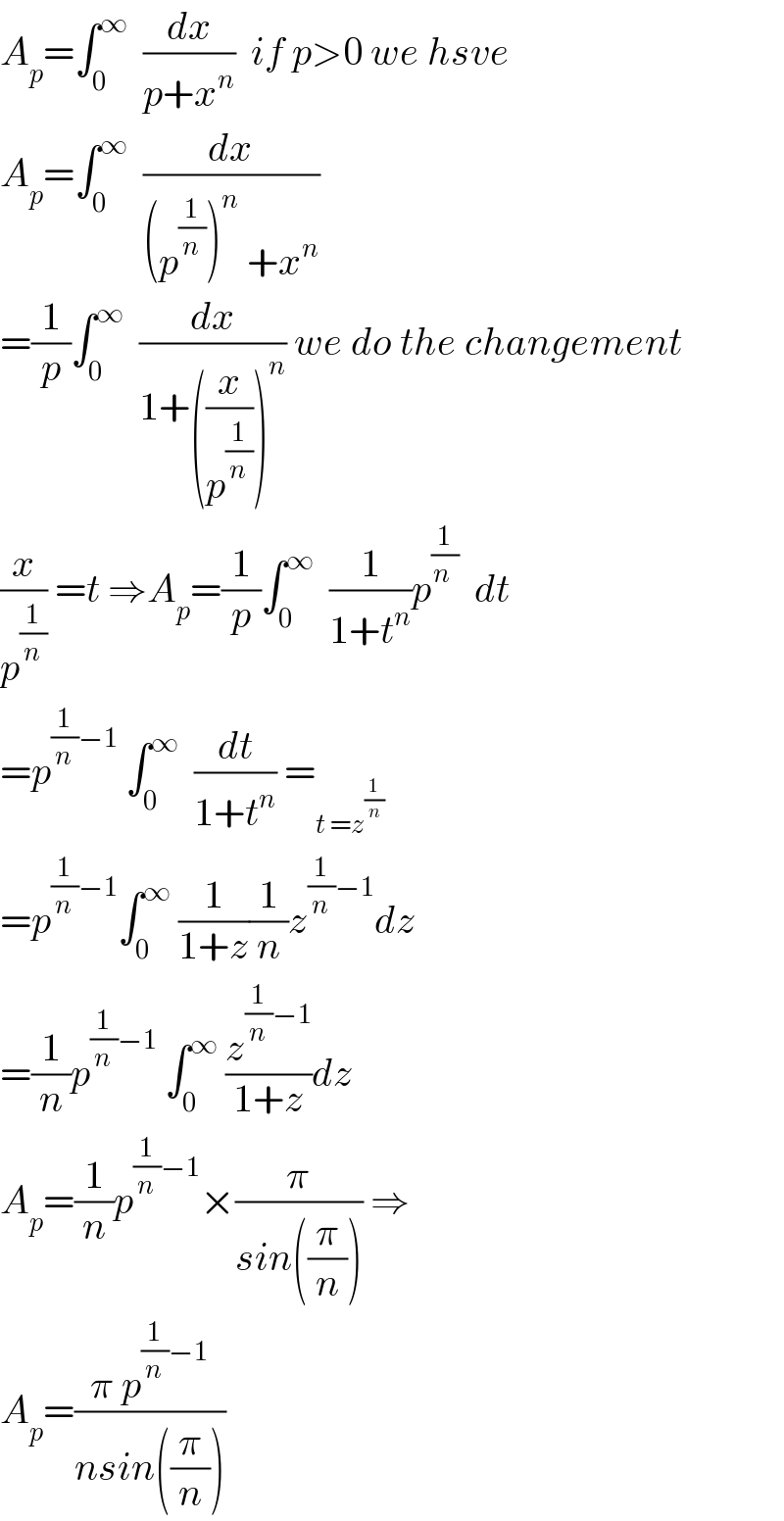
$${A}_{{p}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{p}+{x}^{{n}} }\:\:{if}\:{p}>\mathrm{0}\:{we}\:{hsve} \\ $$$${A}_{{p}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({p}^{\frac{\mathrm{1}}{{n}}} \right)^{{n}} \:+{x}^{{n}} } \\ $$$$=\frac{\mathrm{1}}{{p}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+\left(\frac{{x}}{{p}^{\frac{\mathrm{1}}{{n}}} }\right)^{{n}} }\:{we}\:{do}\:{the}\:{changement} \\ $$$$\frac{{x}}{{p}^{\frac{\mathrm{1}}{{n}}} }\:={t}\:\Rightarrow{A}_{{p}} =\frac{\mathrm{1}}{{p}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{{n}} }{p}^{\frac{\mathrm{1}}{{n}\:}} \:\:{dt} \\ $$$$={p}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\mathrm{1}+{t}^{{n}} }\:=_{{t}\:={z}^{\frac{\mathrm{1}}{{n}}} } \\ $$$$={p}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{1}+{z}}\frac{\mathrm{1}}{{n}}{z}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dz} \\ $$$$=\frac{\mathrm{1}}{{n}}{p}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} \:\frac{{z}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{\mathrm{1}+{z}}{dz} \\ $$$${A}_{{p}} =\frac{\mathrm{1}}{{n}}{p}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} ×\frac{\pi}{{sin}\left(\frac{\pi}{{n}}\right)}\:\Rightarrow \\ $$$${A}_{{p}} =\frac{\pi\:{p}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} }{{nsin}\left(\frac{\pi}{{n}}\right)} \\ $$
Commented by Bird last updated on 12/Oct/20
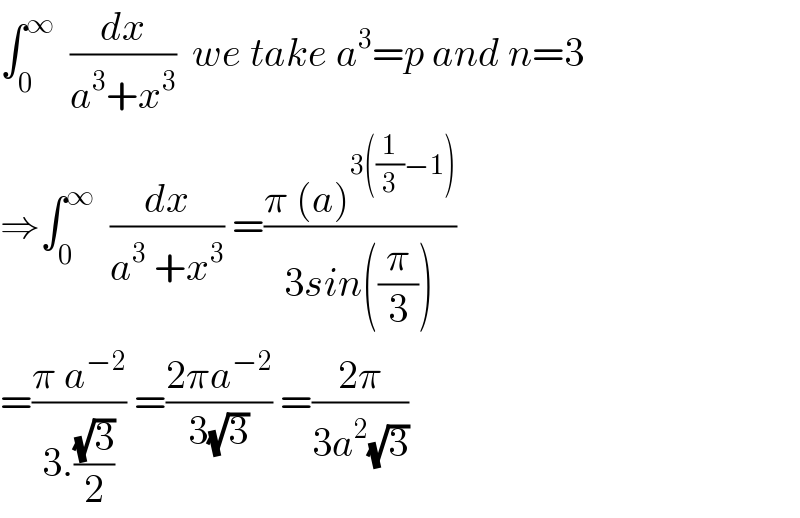
$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{a}^{\mathrm{3}} +{x}^{\mathrm{3}} }\:\:{we}\:{take}\:{a}^{\mathrm{3}} ={p}\:{and}\:{n}=\mathrm{3} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{{a}^{\mathrm{3}} \:+{x}^{\mathrm{3}} }\:=\frac{\pi\:\left({a}\right)^{\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right)} }{\mathrm{3}{sin}\left(\frac{\pi}{\mathrm{3}}\right)} \\ $$$$=\frac{\pi\:{a}^{−\mathrm{2}} }{\mathrm{3}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\mathrm{2}\pi{a}^{−\mathrm{2}} }{\mathrm{3}\sqrt{\mathrm{3}}}\:=\frac{\mathrm{2}\pi}{\mathrm{3}{a}^{\mathrm{2}} \sqrt{\mathrm{3}}} \\ $$
