Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 121659 by Dwaipayan Shikari last updated on 10/Nov/20

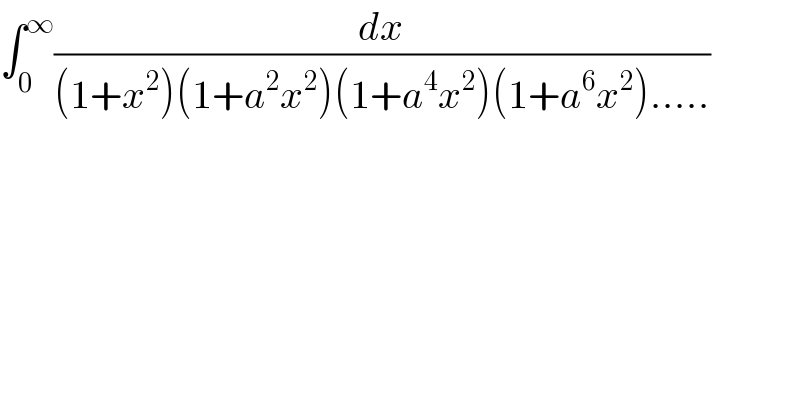
∫_0 ^∞ (dx/((1+x^2 )(1+a^2 x^2 )(1+a^4 x^2 )(1+a^6 x^2 ).....))

$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{4}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{6}} {x}^{\mathrm{2}} \right).....} \\ $$$$ \\ $$

Commented by Dwaipayan Shikari last updated on 10/Nov/20

∫_0 ^∞ (dx/((1+x^2 )(1+a^2 x^2 )))=(π/(2(a+1))) ∫_0 ^∞ (1/((1+x^2 )(1+a^2 x^2 )(1+a^4 x^2 )))=(π/(2(1+a+a^3 ))) ∫_0 ^∞ (1/((1+x^2 )(1+a^2 x^2 )(1+a^4 x^2 )(1+a^6 x^2 )))=(π/(2(1+a+a^3 +a^6 ))) ∫_0 ^∞ (1/((1+x^2 )(1+a^2 x^2 )(1+a^4 x^2 )....))=(π/(2(1+a+a^3 +a^6 +a^(10) +C)))

$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)}=\frac{\pi}{\mathrm{2}\left({a}+\mathrm{1}\right)} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{4}} {x}^{\mathrm{2}} \right)}=\frac{\pi}{\mathrm{2}\left(\mathrm{1}+{a}+{a}^{\mathrm{3}} \right)} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{4}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{6}} {x}^{\mathrm{2}} \right)}=\frac{\pi}{\mathrm{2}\left(\mathrm{1}+{a}+{a}^{\mathrm{3}} +{a}^{\mathrm{6}} \right)} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{a}^{\mathrm{4}} {x}^{\mathrm{2}} \right)....}=\frac{\pi}{\mathrm{2}\left(\mathrm{1}+{a}+{a}^{\mathrm{3}} +{a}^{\mathrm{6}} +{a}^{\mathrm{10}} +{C}\right)} \\ $$

Commented by TANMAY PANACEA last updated on 10/Nov/20

excellent

$${excellent} \\ $$

Commented by Dwaipayan Shikari last updated on 10/Nov/20

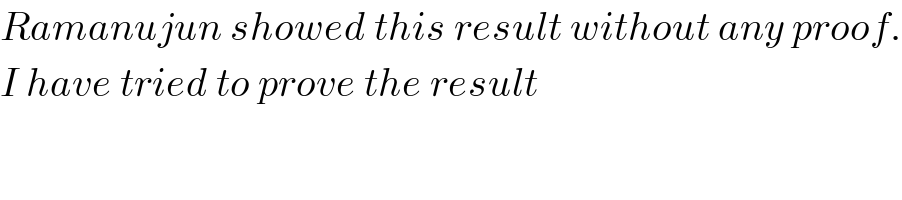
Ramanujun showed this result without any proof. I have tried to prove the result

$${Ramanujun}\:{showed}\:{this}\:{result}\:{without}\:{any}\:{proof}. \\ $$$${I}\:{have}\:{tried}\:{to}\:{prove}\:{the}\:{result} \\ $$

Commented by Dwaipayan Shikari last updated on 10/Nov/20

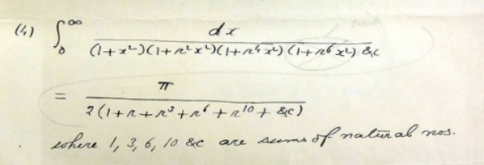
Answered by mindispower last updated on 11/Nov/20

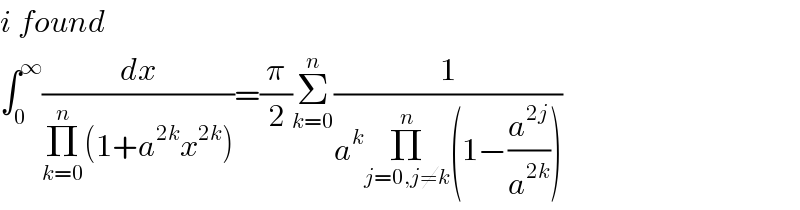
i found ∫_0 ^∞ (dx/(Π_(k=0) ^n (1+a^(2k) x^(2k) )))=(π/2)Σ_(k=0) ^n (1/(a^k Π_(j=0,j≠k) ^n (1−(a^(2j) /a^(2k) ))))

$${i}\:{found} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}\left(\mathrm{1}+{a}^{\mathrm{2}{k}} {x}^{\mathrm{2}{k}} \right)}=\frac{\pi}{\mathrm{2}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{a}^{{k}} \underset{{j}=\mathrm{0},{j}\neq{k}} {\overset{{n}} {\prod}}\left(\mathrm{1}−\frac{{a}^{\mathrm{2}{j}} }{{a}^{\mathrm{2}{k}} }\right)} \\ $$

Commented by Dwaipayan Shikari last updated on 11/Nov/20

x is not varying

$${x}\:{is}\:{not}\:{varying} \\ $$

Answered by mindispower last updated on 11/Nov/20

let f(n)=∫_0 ^∞ (dx/((1+x^2 )......(1+x^2 a^(2n) ))) f(n)=(1/2)∫_(−∞) ^∞ (dx/((1+x^2 ).....(1+x^2 a^(2n) )))=(1/2)∫_(−∞) ^∞ g(x)dx integrat in complex uper half plan Im(z)>0 1+a^(2k) x^2 =0⇒x=+_− (i/a^k ) poles aret_k = (i/a^k ),k∈[0,...n] Res(g,(i/a^k ))=lim_(x→(i/a^k )) (x−(i/a^k ))g(x)=(1/(2ia^k )).Π_(j=0,j≠k) ^n (1/((1−(a^(2j) /a^(2k) )))) f(n)=(1/2).2iπRes(g,t_k ,k∈[0,n]) =(1/2).2iπΣ_(k≤n) (1/(2ia_k ))=(π/2)Σ_(k≤n) (1/a^k ).Π_(j=0,j≠k) ^n (1/((1−((a^j /a^k ))^2 )))

$${let}\:{f}\left({n}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)......\left(\mathrm{1}+{x}^{\mathrm{2}} {a}^{\mathrm{2}{n}} \right)} \\ $$$${f}\left({n}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} \frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right).....\left(\mathrm{1}+{x}^{\mathrm{2}} {a}^{\mathrm{2}{n}} \right)}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} {g}\left({x}\right){dx} \\ $$$${integrat}\:{in}\:{complex}\:{uper}\:{half}\:{plan}\:{Im}\left({z}\right)>\mathrm{0} \\ $$$$\mathrm{1}+{a}^{\mathrm{2}{k}} {x}^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\underset{−} {+}\frac{{i}}{{a}^{{k}} } \\ $$$${poles}\:{aret}_{{k}} =\:\frac{{i}}{{a}^{{k}} },{k}\in\left[\mathrm{0},...{n}\right] \\ $$$${Res}\left({g},\frac{{i}}{{a}^{{k}} }\right)=\underset{{x}\rightarrow\frac{{i}}{{a}^{{k}} }} {\mathrm{lim}}\left({x}−\frac{{i}}{{a}^{{k}} }\right){g}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{ia}^{{k}} }.\underset{{j}=\mathrm{0},{j}\neq{k}} {\overset{{n}} {\prod}}\frac{\mathrm{1}}{\left(\mathrm{1}−\frac{{a}^{\mathrm{2}{j}} }{{a}^{\mathrm{2}{k}} }\right)} \\ $$$${f}\left({n}\right)=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{i}\pi{Res}\left({g},{t}_{{k}} ,{k}\in\left[\mathrm{0},{n}\right]\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{i}\pi\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{\mathrm{2}{ia}_{{k}} }=\frac{\pi}{\mathrm{2}}\underset{{k}\leqslant{n}} {\sum}\frac{\mathrm{1}}{{a}^{{k}} }.\underset{{j}=\mathrm{0},{j}\neq{k}} {\overset{{n}} {\prod}}\frac{\mathrm{1}}{\left(\mathrm{1}−\left(\frac{{a}^{{j}} }{{a}^{{k}} }\right)^{\mathrm{2}} \right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com