Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 134546 by mohammad17 last updated on 05/Mar/21

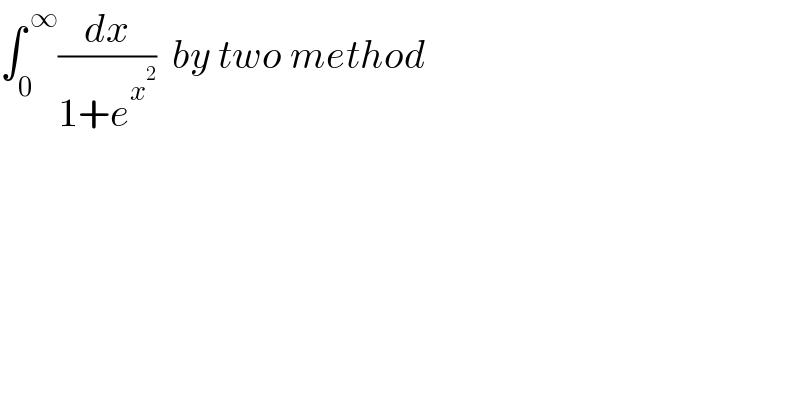
∫_0 ^( ∞) (dx/(1+e^x^2 )) by two method

$$\int_{\mathrm{0}} ^{\:\infty} \frac{{dx}}{\mathrm{1}+{e}^{{x}^{\mathrm{2}} } }\:\:{by}\:{two}\:{method} \\ $$

Answered by Dwaipayan Shikari last updated on 05/Mar/21

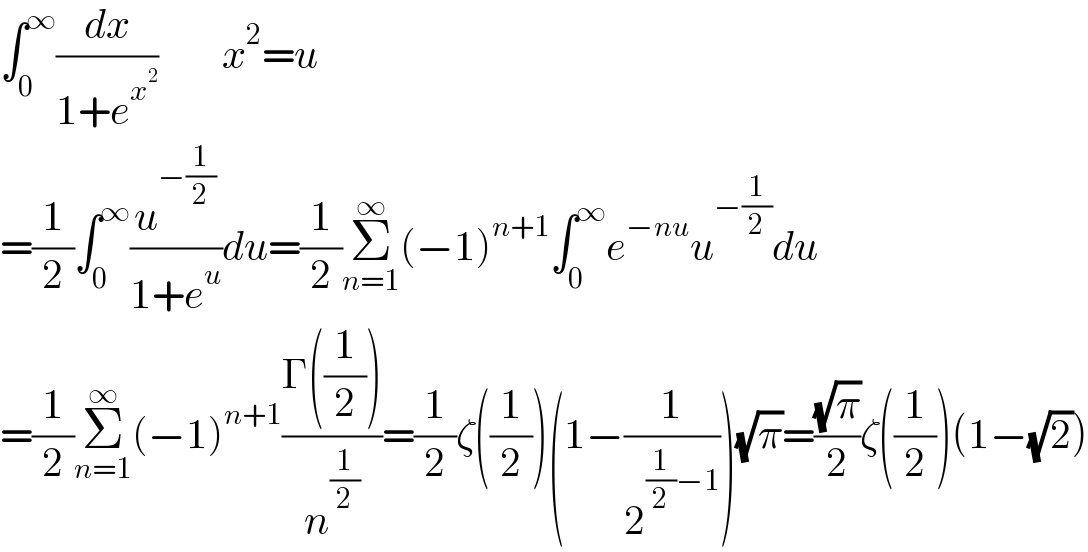
∫_0 ^∞ (dx/(1+e^x^2 )) x^2 =u =(1/2)∫_0 ^∞ (u^(−(1/2)) /(1+e^u ))du=(1/2)Σ_(n=1) ^∞ (−1)^(n+1) ∫_0 ^∞ e^(−nu) u^(−(1/2)) du =(1/2)Σ_(n=1) ^∞ (−1)^(n+1) ((Γ((1/2)))/n^(1/2) )=(1/2)ζ((1/2))(1−(1/2^((1/2)−1) ))(√π)=((√π)/2)ζ((1/2))(1−(√2))

$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{e}^{{x}^{\mathrm{2}} } }\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} ={u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+{e}^{{u}} }{du}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \int_{\mathrm{0}} ^{\infty} {e}^{−{nu}} {u}^{−\frac{\mathrm{1}}{\mathrm{2}}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{{n}^{\frac{\mathrm{1}}{\mathrm{2}}} }=\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }\right)\sqrt{\pi}=\frac{\sqrt{\pi}}{\mathrm{2}}\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{1}−\sqrt{\mathrm{2}}\right) \\ $$

Commented by mohammad17 last updated on 05/Mar/21

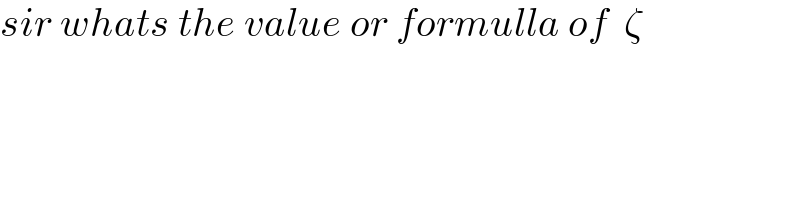
sir whats the value or formulla of ζ

$${sir}\:{whats}\:{the}\:{value}\:{or}\:{formulla}\:{of}\:\:\zeta \\ $$

Commented by Dwaipayan Shikari last updated on 05/Mar/21

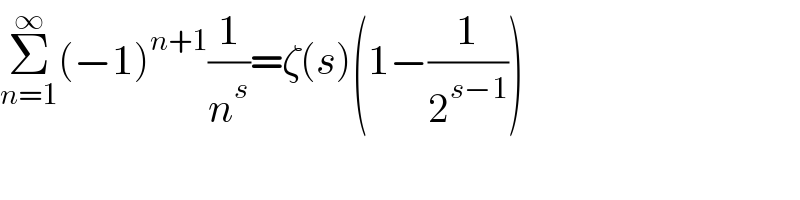
Σ_(n=1) ^∞ (−1)^(n+1) (1/n^s )=ζ(s)(1−(1/2^(s−1) ))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}^{{s}} }=\zeta\left({s}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{s}−\mathrm{1}} }\right) \\ $$

Answered by mathmax by abdo last updated on 05/Mar/21

Φ =∫_0 ^∞ (dx/(1+e^x^2 )) we do the changement x^2 =t ⇒ Φ =∫_0 ^∞ (dt/(2(√t)(1+e^t ))) =(1/2)∫_0 ^∞ (t^(−(1/2)) /(1+e^t ))dt =(1/2)∫_0 ^∞ ((t^(−(1/2)) e^(−t) )/(1+e^(−t) ))dt =(1/2)∫_0 ^∞ t^(−(1/2)) e^(−t) Σ_(n=0) ^∞ (−1)^n e^(−nt) dt =(1/2)Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ t^(−(1/2)) e^(−(n+1)t) dt =_((n+1)t=z) (1/2)Σ_(n=0) ^(∞ ) (−1)^n ∫_0 ^∞ ((z/(n+1)))^(−(1/2)) e^(−z) (dz/(n+1)) =(1/2)Σ_(n=0) ^∞ (−1)^n (1/((n+1)^(1/2) ))∫_0 ^∞ z^(−(1/2)) e^(−z) dz =((Γ((1/2)))/2)Σ_(n=1) ^(∞ ) (((−1)^(n−1) )/n^(1/2) ) =−(1/2)(√π)δ((1/2)) δ(x)=Σ_(n=1) ^∞ (((−1)^n )/n^x ) =(2^(1−x) −1)ξ(x) ⇒δ((1/2))=(2^(1/2) −1)ξ((1/2)) =((√2)−1)ξ((1/2))....

$$\Phi\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } }\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}^{\mathrm{2}} =\mathrm{t}\:\Rightarrow \\ $$$$\Phi\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{t}}\left(\mathrm{1}+\mathrm{e}^{\mathrm{t}} \right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+\mathrm{e}^{\mathrm{t}} }\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{t}} }{\mathrm{1}+\mathrm{e}^{−\mathrm{t}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{t}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{nt}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} \:\mathrm{dt} \\ $$$$=_{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}=\mathrm{z}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{z}}{\mathrm{n}+\mathrm{1}}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{z}} \:\frac{\mathrm{dz}}{\mathrm{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{z}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{z}} \:\mathrm{dz} \\ $$$$=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty\:} \:\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\frac{\mathrm{1}}{\mathrm{2}}} }\:=−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi}\delta\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\delta\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{x}} }\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{x}} −\mathrm{1}\right)\xi\left(\mathrm{x}\right)\:\Rightarrow\delta\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\left(\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}\right)\xi\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\xi\left(\frac{\mathrm{1}}{\mathrm{2}}\right).... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com