
Question Number 132954 by LUFFY last updated on 17/Feb/21
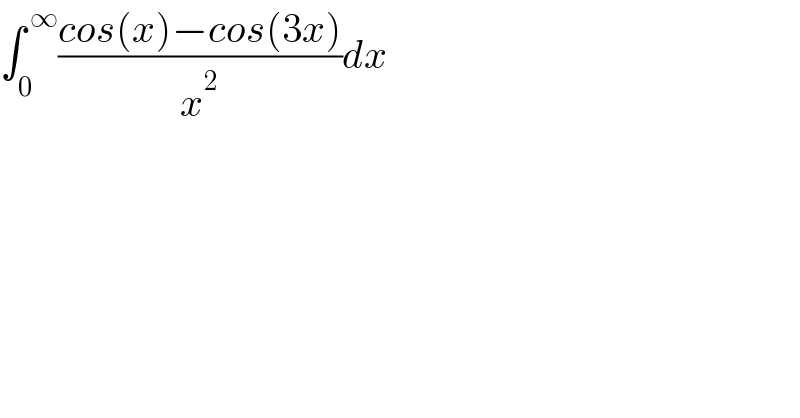
$$\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left({x}\right)−{cos}\left(\mathrm{3}{x}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 17/Feb/21
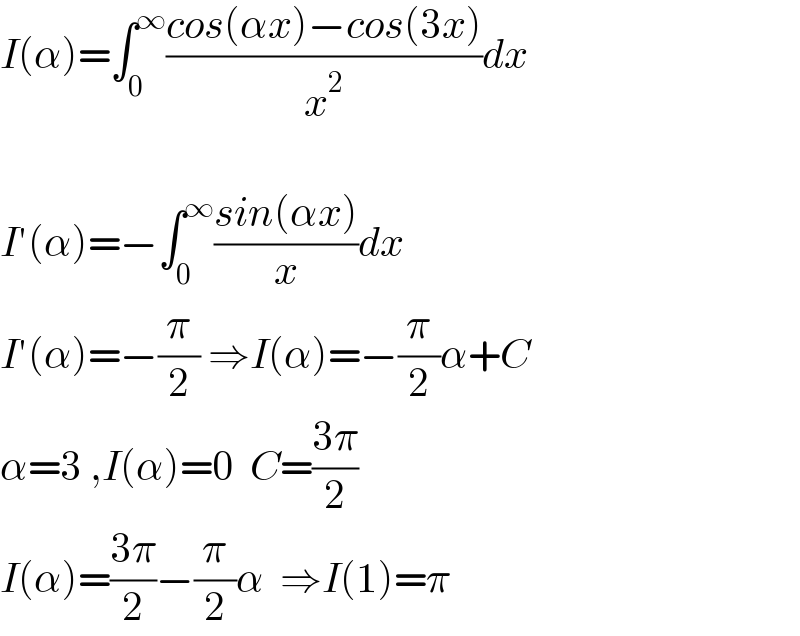
$${I}\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left(\alpha{x}\right)−{cos}\left(\mathrm{3}{x}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$$$ \\ $$$${I}'\left(\alpha\right)=−\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left(\alpha{x}\right)}{{x}}{dx} \\ $$$${I}'\left(\alpha\right)=−\frac{\pi}{\mathrm{2}}\:\Rightarrow{I}\left(\alpha\right)=−\frac{\pi}{\mathrm{2}}\alpha+{C} \\ $$$$\alpha=\mathrm{3}\:,{I}\left(\alpha\right)=\mathrm{0}\:\:{C}=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$${I}\left(\alpha\right)=\frac{\mathrm{3}\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\alpha\:\:\Rightarrow{I}\left(\mathrm{1}\right)=\pi \\ $$
