Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 218582 by Nicholas666 last updated on 12/Apr/25

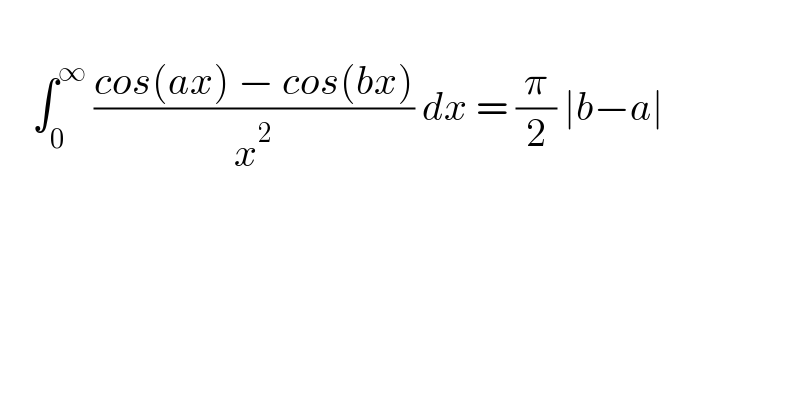
∫_0 ^∞ ((cos(ax) − cos(bx))/x^2 ) dx = (π/2) ∣b−a∣

$$ \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left({ax}\right)\:−\:{cos}\left({bx}\right)}{{x}^{\mathrm{2}} }\:{dx}\:=\:\frac{\pi}{\mathrm{2}}\:\mid{b}−{a}\mid\: \\ $$$$ \\ $$

Answered by aleks041103 last updated on 12/Apr/25

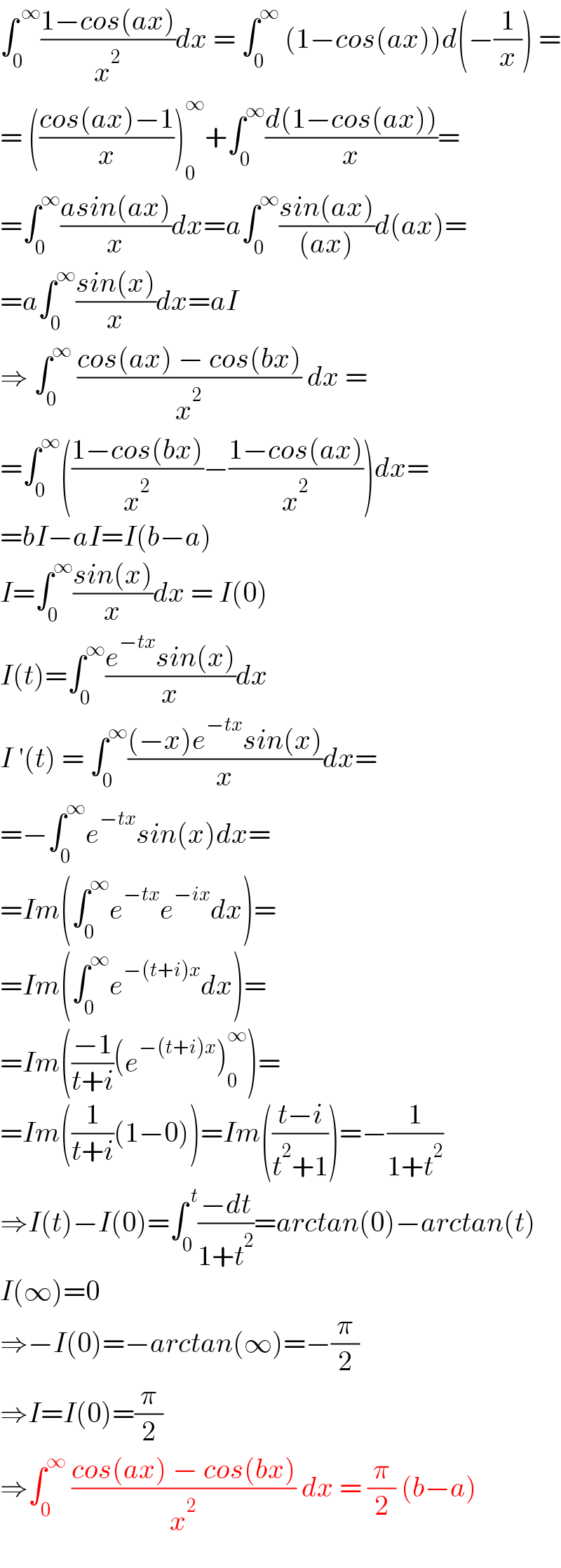
∫_0 ^( ∞) ((1−cos(ax))/x^2 )dx = ∫_0 ^∞ (1−cos(ax))d(−(1/x)) = = (((cos(ax)−1)/x))_0 ^∞ +∫_0 ^∞ ((d(1−cos(ax)))/x)= =∫_0 ^∞ ((asin(ax))/x)dx=a∫_0 ^∞ ((sin(ax))/((ax)))d(ax)= =a∫_0 ^∞ ((sin(x))/x)dx=aI ⇒ ∫_0 ^∞ ((cos(ax) − cos(bx))/x^2 ) dx = =∫_0 ^∞ (((1−cos(bx))/x^2 )−((1−cos(ax))/x^2 ))dx= =bI−aI=I(b−a) I=∫_0 ^∞ ((sin(x))/x)dx = I(0) I(t)=∫_0 ^∞ ((e^(−tx) sin(x))/x)dx I ′(t) = ∫_0 ^∞ (((−x)e^(−tx) sin(x))/x)dx= =−∫_0 ^∞ e^(−tx) sin(x)dx= =Im(∫_0 ^∞ e^(−tx) e^(−ix) dx)= =Im(∫_0 ^∞ e^(−(t+i)x) dx)= =Im(((−1)/(t+i))(e^(−(t+i)x) )_0 ^∞ )= =Im((1/(t+i))(1−0))=Im(((t−i)/(t^2 +1)))=−(1/(1+t^2 )) ⇒I(t)−I(0)=∫_0 ^( t) ((−dt)/(1+t^2 ))=arctan(0)−arctan(t) I(∞)=0 ⇒−I(0)=−arctan(∞)=−(π/2) ⇒I=I(0)=(π/2) ⇒∫_0 ^∞ ((cos(ax) − cos(bx))/x^2 ) dx = (π/2) (b−a)

$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}−{cos}\left({ax}\right)}{{x}^{\mathrm{2}} }{dx}\:=\:\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{1}−{cos}\left({ax}\right)\right){d}\left(−\frac{\mathrm{1}}{{x}}\right)\:= \\ $$$$=\:\left(\frac{{cos}\left({ax}\right)−\mathrm{1}}{{x}}\right)_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \frac{{d}\left(\mathrm{1}−{cos}\left({ax}\right)\right)}{{x}}= \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{asin}\left({ax}\right)}{{x}}{dx}={a}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({ax}\right)}{\left({ax}\right)}{d}\left({ax}\right)= \\ $$$$={a}\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{{x}}{dx}={aI} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left({ax}\right)\:−\:{cos}\left({bx}\right)}{{x}^{\mathrm{2}} }\:{dx}\:= \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}−{cos}\left({bx}\right)}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}−{cos}\left({ax}\right)}{{x}^{\mathrm{2}} }\right){dx}= \\ $$$$={bI}−{aI}={I}\left({b}−{a}\right) \\ $$$${I}=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({x}\right)}{{x}}{dx}\:=\:{I}\left(\mathrm{0}\right) \\ $$$${I}\left({t}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{tx}} {sin}\left({x}\right)}{{x}}{dx} \\ $$$${I}\:'\left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\left(−{x}\right){e}^{−{tx}} {sin}\left({x}\right)}{{x}}{dx}= \\ $$$$=−\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} {sin}\left({x}\right){dx}= \\ $$$$={Im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}} {e}^{−{ix}} {dx}\right)= \\ $$$$={Im}\left(\int_{\mathrm{0}} ^{\infty} {e}^{−\left({t}+{i}\right){x}} {dx}\right)= \\ $$$$={Im}\left(\frac{−\mathrm{1}}{{t}+{i}}\left({e}^{−\left({t}+{i}\right){x}} \right)_{\mathrm{0}} ^{\infty} \right)= \\ $$$$={Im}\left(\frac{\mathrm{1}}{{t}+{i}}\left(\mathrm{1}−\mathrm{0}\right)\right)={Im}\left(\frac{{t}−{i}}{{t}^{\mathrm{2}} +\mathrm{1}}\right)=−\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow{I}\left({t}\right)−{I}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\:{t}} \frac{−{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }={arctan}\left(\mathrm{0}\right)−{arctan}\left({t}\right) \\ $$$${I}\left(\infty\right)=\mathrm{0} \\ $$$$\Rightarrow−{I}\left(\mathrm{0}\right)=−{arctan}\left(\infty\right)=−\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{I}={I}\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{{cos}\left({ax}\right)\:−\:{cos}\left({bx}\right)}{{x}^{\mathrm{2}} }\:{dx}\:=\:\frac{\pi}{\mathrm{2}}\:\left({b}−{a}\right) \\ $$

Commented by Nicholas666 last updated on 12/Apr/25

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com