
Question Number 221838 by Ghisom last updated on 11/Jun/25
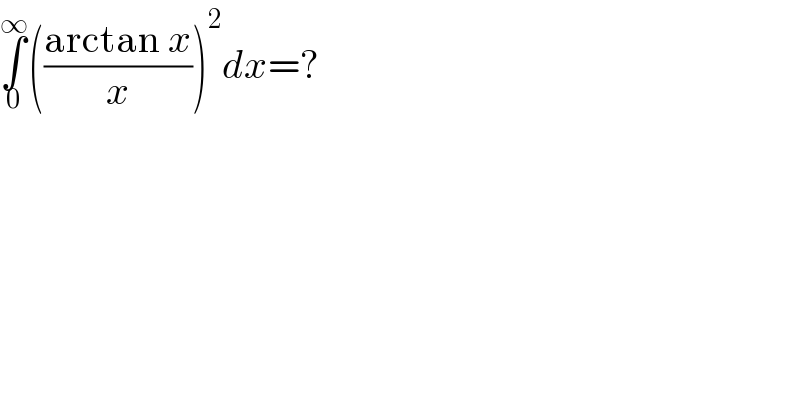
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\left(\frac{\mathrm{arctan}\:{x}}{{x}}\right)^{\mathrm{2}} {dx}=? \\ $$
Answered by wewji12 last updated on 11/Jun/25
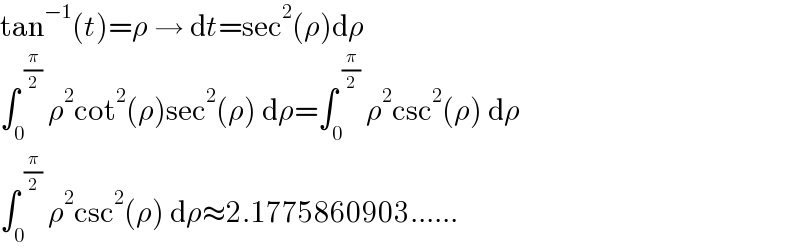
$$\mathrm{tan}^{−\mathrm{1}} \left({t}\right)=\rho\:\rightarrow\:\mathrm{d}{t}=\mathrm{sec}^{\mathrm{2}} \left(\rho\right)\mathrm{d}\rho \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\rho^{\mathrm{2}} \mathrm{cot}^{\mathrm{2}} \left(\rho\right)\mathrm{sec}^{\mathrm{2}} \left(\rho\right)\:\mathrm{d}\rho=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\rho^{\mathrm{2}} \mathrm{csc}^{\mathrm{2}} \left(\rho\right)\:\mathrm{d}\rho \\ $$$$\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \:\rho^{\mathrm{2}} \mathrm{csc}^{\mathrm{2}} \left(\rho\right)\:\mathrm{d}\rho\approx\mathrm{2}.\mathrm{1775860903}...... \\ $$
Commented by Ghisom last updated on 11/Jun/25

$$\mathrm{using}\:\mathrm{software}\:\mathrm{to}\:\mathrm{get}\:\mathrm{an}\:\mathrm{approximation} \\ $$$$\mathrm{is}\:\mathrm{possible}\:\mathrm{without}\:\mathrm{substitution} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{boring} \\ $$$$\mathrm{exact}\:\mathrm{solution}\:\mathrm{required} \\ $$
Answered by Frix last updated on 11/Jun/25
![∫_0 ^∞ (((tan^(−1) x)/x))^2 dx Using Feynman′s Trick twice: ∫_0 ^∞ ((tan^(−1) ax)/x)×((tan^(−1) bx)/x)dx Partially differentiating twice ∫_0 ^∞ (dx/((a^2 x^2 +1)(b^2 x^2 +1)))= =(1/(a^2 −b^2 ))[atan^(−1) ax −btan^(−1) bx]_0 ^∞ = =(π/(2(a+b))) ∫_0 ^∞ (((tan^(−1) x)/x))^2 dx=∫_0 ^1 ∫_0 ^1 (π/(2(a+b)))dadb= =πln 2](Q221867.png)
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\left(\frac{\mathrm{tan}^{−\mathrm{1}} \:{x}}{{x}}\right)^{\mathrm{2}} {dx} \\ $$$$\mathrm{Using}\:\mathrm{Feynman}'\mathrm{s}\:\mathrm{Trick}\:\mathrm{twice}: \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{tan}^{−\mathrm{1}} \:{ax}}{{x}}×\frac{\mathrm{tan}^{−\mathrm{1}} \:{bx}}{{x}}{dx} \\ $$$$\mathrm{Partially}\:\mathrm{differentiating}\:\mathrm{twice} \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dx}}{\left({a}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }\left[{a}\mathrm{tan}^{−\mathrm{1}} \:{ax}\:−{b}\mathrm{tan}^{−\mathrm{1}} \:{bx}\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=\frac{\pi}{\mathrm{2}\left({a}+{b}\right)} \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\left(\frac{\mathrm{tan}^{−\mathrm{1}} \:{x}}{{x}}\right)^{\mathrm{2}} {dx}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\pi}{\mathrm{2}\left({a}+{b}\right)}{dadb}= \\ $$$$=\pi\mathrm{ln}\:\mathrm{2} \\ $$
Commented by Ghisom last updated on 11/Jun/25
��
Commented by wewji12 last updated on 12/Jun/25

$$\mathrm{Wow}\:\mathrm{great}!!!! \\ $$
