
Question Number 76956 by behi83417@gmail.com last updated on 01/Jan/20
![∫_( 0) ^( a) (dx/(√((a+sinx)(a+cosx)))) =? [a∈R^+ ,test for: a=1]](Q76956.png)
$$\underset{\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{a}}} {\int}}\:\:\:\frac{\boldsymbol{\mathrm{dx}}}{\sqrt{\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{sinx}}\right)\left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{cosx}}\right)}}\:=? \\ $$$$\left[\boldsymbol{\mathrm{a}}\in\boldsymbol{\mathrm{R}}^{+} ,\boldsymbol{\mathrm{test}}\:\boldsymbol{\mathrm{for}}:\:\:\boldsymbol{\mathrm{a}}=\mathrm{1}\right] \\ $$
Answered by john santu last updated on 02/Jan/20
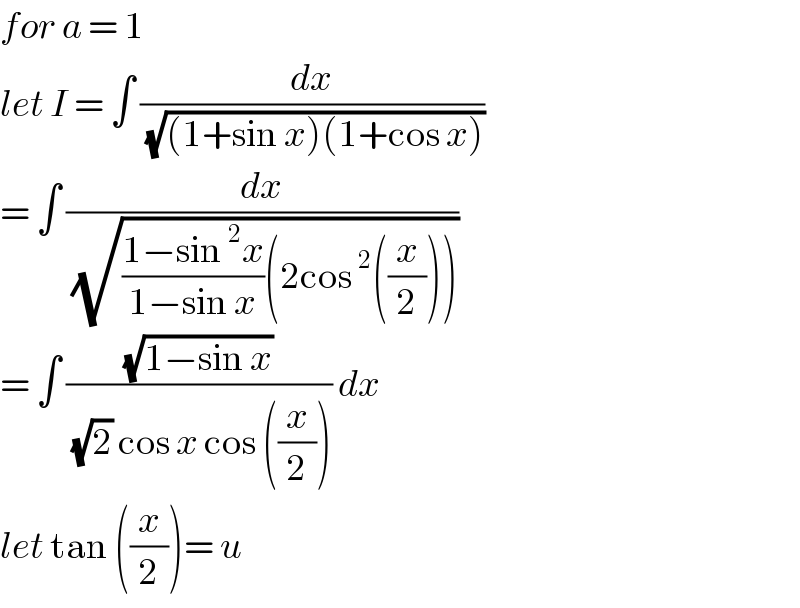
$${for}\:{a}\:=\:\mathrm{1}\: \\ $$$${let}\:{I}\:=\:\int\:\frac{{dx}}{\sqrt{\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\left(\mathrm{1}+\mathrm{cos}\:{x}\right)}} \\ $$$$=\:\int\:\frac{{dx}}{\sqrt{\frac{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{1}−\mathrm{sin}\:{x}}\left(\mathrm{2cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)}} \\ $$$$=\:\int\:\frac{\sqrt{\mathrm{1}−\mathrm{sin}\:{x}}}{\sqrt{\mathrm{2}}\:\mathrm{cos}\:{x}\:\mathrm{cos}\:\left(\frac{{x}}{\mathrm{2}}\right)}\:{dx} \\ $$$${let}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)=\:{u}\: \\ $$
