
Question Number 94312 by i jagooll last updated on 18/May/20
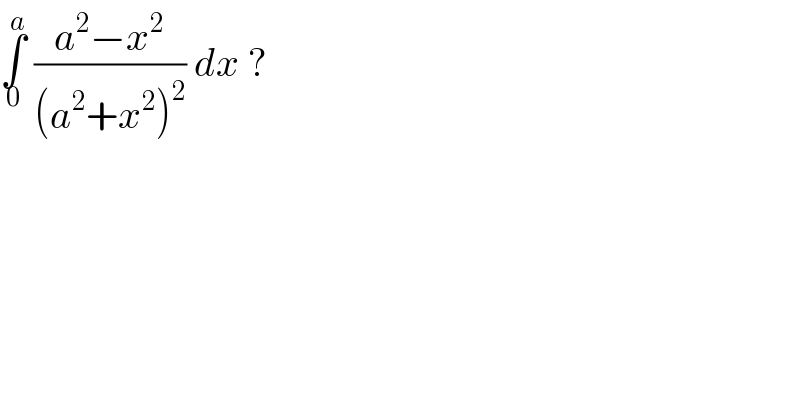
$$\underset{\mathrm{0}} {\overset{{a}} {\int}}\:\frac{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}\:? \\ $$
Commented by mathmax by abdo last updated on 18/May/20
![let I =∫_0 ^a ((a^2 −x^2 )/((a^2 +x^2 )^2 ))dx ⇒I =_(x=at) ∫_0 ^1 ((a^2 −a^2 t^2 )/(a^4 (1+t^2 )^2 )) ×adt =(1/a) ∫_0 ^1 ((1−t^2 )/((1+t^2 )^2 ))dt ⇒aI =∫_0 ^1 ((1+t^2 −2t^2 )/((1+t^2 )^2 ))dt =∫_0 ^1 (dt/(1+t^2 )) −2 ∫_0 ^1 (t^2 /((1+t^2 )^2 ))dt we have ∫_0 ^1 (dt/(1+t^2 )) =[arctant]_0 ^1 =(π/4) ∫_0 ^1 (t^2 /((1+t^2 )^2 ))dt =∫_0 ^1 ((1+t^2 −1)/((1+t^2 )^2 ))dt =∫_0 ^1 (dt/(1+t^2 ))−∫_0 ^1 (dt/((1+t^2 )^2 )) =(π/4)−∫_0 ^1 (dt/((1+t^2 )^2 )) ∫_0 ^1 (dt/((1+t^2 )^2 )) =_(t=tanu) ∫_0 ^(π/4) ((1+tan^2 u)/((1+tan^2 u)^2 ))du =∫_0 ^(π/4) (du/(1+tan^2 u)) =∫_0 ^(π/4) cos^2 udu =(1/2)∫_0 ^(π/2) (1+cos(2u))du =(π/4) +(1/4)[sin(2u)]_0 ^(π/4) =(π/4)+(1/4) ⇒aI =(π/4) −2{(π/4)−(π/4)−(1/4)} =(π/4) +(1/2) ⇒I =(1/a)((π/4)+(1/2)) with a≠0 for a=0 I is not defined !](Q94315.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{{a}} \:\frac{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow{I}\:=_{{x}={at}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{a}^{\mathrm{2}} −{a}^{\mathrm{2}} {t}^{\mathrm{2}} }{{a}^{\mathrm{4}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:×{adt} \\ $$$$=\frac{\mathrm{1}}{{a}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:\Rightarrow{aI}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:\:{we}\:{have}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\left[{arctant}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{4}}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=_{{t}={tanu}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+{tan}^{\mathrm{2}} {u}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {u}\right)^{\mathrm{2}} }{du}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{du}}{\mathrm{1}+{tan}^{\mathrm{2}} {u}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {cos}^{\mathrm{2}} {udu}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+{cos}\left(\mathrm{2}{u}\right)\right){du}\:=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sin}\left(\mathrm{2}{u}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{aI}\:=\frac{\pi}{\mathrm{4}}\:−\mathrm{2}\left\{\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\right\} \\ $$$$=\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{I}\:=\frac{\mathrm{1}}{{a}}\left(\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:\:\:{with}\:{a}\neq\mathrm{0}\: \\ $$$${for}\:{a}=\mathrm{0}\:{I}\:{is}\:{not}\:{defined}\:! \\ $$
Commented by mathmax by abdo last updated on 18/May/20
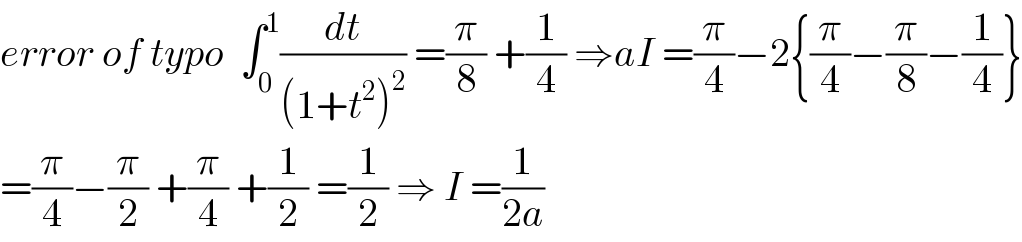
$${error}\:{of}\:{typo}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{aI}\:=\frac{\pi}{\mathrm{4}}−\mathrm{2}\left\{\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{4}}\right\} \\ $$$$=\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}{a}} \\ $$
Commented by i jagooll last updated on 18/May/20

$$\mathrm{yes}.=== \\ $$
