
Question Number 37036 by ajfour last updated on 08/Jun/18
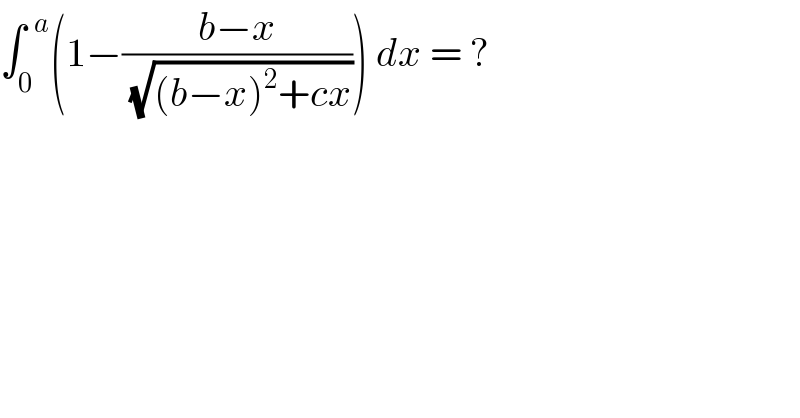
$$\int_{\mathrm{0}} ^{\:\:{a}} \left(\mathrm{1}−\frac{{b}−{x}}{\sqrt{\left({b}−{x}\right)^{\mathrm{2}} +{cx}}}\right)\:{dx}\:=\:? \\ $$
Commented by math khazana by abdo last updated on 09/Jun/18
![I =a −(1/2)∫_0 ^a ((2(b−x) +2c)/(√((b−x)^2 +c)))dx =a −∫_0 ^a ((2(b−x) +c)/(2(√((b−x)^2 +cx))))dx −(c/2) ∫_0 ^a (dx/(√((b−x)^2 +cx))) =a−(√((b−x)^2 +cx)) −(c/2) ∫_0 ^a (dx/(√(x^2 −2bx +b^2 +cx))) but x^2 −2bx +b^2 +cx = x^2 +(c−2b)x +b^2 = x^2 +2 ((c−2b)/2) x + (((c−2b)^2 )/4) +b^2 −(((c−2b)^2 )/4) =(x +((c−2b)/2))^2 + ((4b^2 −c^2 +4bc −4b^2 )/4) =(x +((c−2b)/2))^2 + ((4bc −c^2 )/4) case 1 if 4bc −c^2 >0 we use the changement x+ ((c−2b)/2) =((√(4bc−c^2 ))/2) t and ∫_0 ^a (dx/(√(x^2 +(c−2b)x +b^2 ))) = ∫_((c−2b)/(√(4bc−c^2 ))) ^((2a+c−b)/(√(4bc−c^2 ))) (1/(((√(4bc−c^2 ))/2)(√(1+t^2 )))) ((√(4bc−c^2 ))/2)dt = [argsht]_((c−2b)/(√(4bc−c^2 ))) ^((2a+c−b)/(√(4bc−c^2 ))) =ln( ((2a+c)/(√(4bc−c^2 ))) +(√(1+(((2a+c)/(√(4bc−c^2 ))))^2 )) ) −ln( ((c−2b)/(√(4bc−c^2 ))) +(√(1+(((c−2b)/(√(4bc−c^2 ))))^2 ))) =A so I = a−(√((b−x)^2 +cx)) −(c/2) A case2 4bc−c^2 <0 ⇒(x +((c−2b)/2))^2 +((4bc−c^2 )/4) =(x +((c−2b)/2))^2 − ((√((c^2 −4bc)/4)))^2 and we use the chang. x+((c−2b)/2) =((√(c^2 −4bc))/2) u ...be continued...](Q37105.png)
$${I}\:={a}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{a}} \:\:\:\frac{\mathrm{2}\left({b}−{x}\right)\:+\mathrm{2}{c}}{\sqrt{\left({b}−{x}\right)^{\mathrm{2}} \:+{c}}}{dx} \\ $$$$={a}\:−\int_{\mathrm{0}} ^{{a}} \:\:\:\:\:\:\frac{\mathrm{2}\left({b}−{x}\right)\:+{c}}{\mathrm{2}\sqrt{\left({b}−{x}\right)^{\mathrm{2}} \:+{cx}}}{dx}\:−\frac{{c}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{a}} \:\:\:\:\:\frac{{dx}}{\sqrt{\left({b}−{x}\right)^{\mathrm{2}} \:+{cx}}} \\ $$$$={a}−\sqrt{\left({b}−{x}\right)^{\mathrm{2}} \:+{cx}}\:\:−\frac{{c}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{a}} \:\:\:\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} \:−\mathrm{2}{bx}\:+{b}^{\mathrm{2}} \:+{cx}}} \\ $$$${but}\:{x}^{\mathrm{2}} \:−\mathrm{2}{bx}\:+{b}^{\mathrm{2}} \:+{cx}\:=\:{x}^{\mathrm{2}} \:+\left({c}−\mathrm{2}{b}\right){x}\:+{b}^{\mathrm{2}} \\ $$$$=\:{x}^{\mathrm{2}} \:\:+\mathrm{2}\:\frac{{c}−\mathrm{2}{b}}{\mathrm{2}}\:{x}\:+\:\frac{\left({c}−\mathrm{2}{b}\right)^{\mathrm{2}} }{\mathrm{4}}\:+{b}^{\mathrm{2}} \:−\frac{\left({c}−\mathrm{2}{b}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\left({x}\:+\frac{{c}−\mathrm{2}{b}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\:\frac{\mathrm{4}{b}^{\mathrm{2}} \:−{c}^{\mathrm{2}} \:+\mathrm{4}{bc}\:−\mathrm{4}{b}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\left({x}\:+\frac{{c}−\mathrm{2}{b}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:+\:\frac{\mathrm{4}{bc}\:−{c}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${case}\:\mathrm{1}\:\:{if}\:\mathrm{4}{bc}\:−{c}^{\mathrm{2}} >\mathrm{0}\:{we}\:{use}\:{the}\:{changement} \\ $$$${x}+\:\frac{{c}−\mathrm{2}{b}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}{\mathrm{2}}\:{t}\:\:\:{and} \\ $$$$\int_{\mathrm{0}} ^{{a}} \:\:\:\:\:\frac{{dx}}{\sqrt{{x}^{\mathrm{2}} \:+\left({c}−\mathrm{2}{b}\right){x}\:+{b}^{\mathrm{2}} }}\:=\:\int_{\frac{{c}−\mathrm{2}{b}}{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}} ^{\frac{\mathrm{2}{a}+{c}−{b}}{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}} \:\:\:\:\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}{\mathrm{2}}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}{\mathrm{2}}{dt} \\ $$$$=\:\left[{argsht}\right]_{\frac{{c}−\mathrm{2}{b}}{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}} ^{\frac{\mathrm{2}{a}+{c}−{b}}{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} \:}}} \:\:\:\:={ln}\left(\:\frac{\mathrm{2}{a}+{c}}{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{a}+{c}}{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}\right)^{\mathrm{2}} }\:\right) \\ $$$$−{ln}\left(\:\frac{{c}−\mathrm{2}{b}}{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}\:+\sqrt{\mathrm{1}+\left(\frac{{c}−\mathrm{2}{b}}{\sqrt{\mathrm{4}{bc}−{c}^{\mathrm{2}} }}\right)^{\mathrm{2}} }\right)\:={A}\:{so} \\ $$$${I}\:=\:{a}−\sqrt{\left({b}−{x}\right)^{\mathrm{2}} \:+{cx}}\:\:−\frac{{c}}{\mathrm{2}}\:{A} \\ $$$${case}\mathrm{2}\:\mathrm{4}{bc}−{c}^{\mathrm{2}} <\mathrm{0}\:\Rightarrow\left({x}\:+\frac{{c}−\mathrm{2}{b}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}{bc}−{c}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\left({x}\:+\frac{{c}−\mathrm{2}{b}}{\mathrm{2}}\right)^{\mathrm{2}} \:−\:\left(\sqrt{\frac{{c}^{\mathrm{2}} −\mathrm{4}{bc}}{\mathrm{4}}}\right)^{\mathrm{2}} \:{and}\:{we}\:{use} \\ $$$${the}\:{chang}.\:{x}+\frac{{c}−\mathrm{2}{b}}{\mathrm{2}}\:=\frac{\sqrt{{c}^{\mathrm{2}} \:−\mathrm{4}{bc}}}{\mathrm{2}}\:\:\:{u}\:\:...{be}\:{continued}... \\ $$
Commented by ajfour last updated on 09/Jun/18
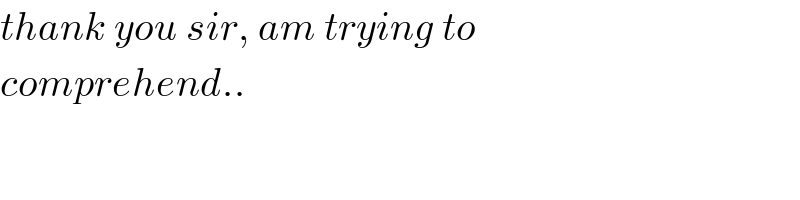
$${thank}\:{you}\:{sir},\:{am}\:{trying}\:{to} \\ $$$${comprehend}.. \\ $$
Commented by math khazana by abdo last updated on 09/Jun/18
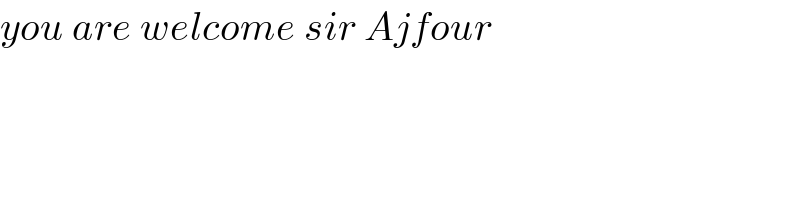
$${you}\:{are}\:{welcome}\:{sir}\:{Ajfour} \\ $$
