
Question Number 186854 by liuxinnan last updated on 11/Feb/23
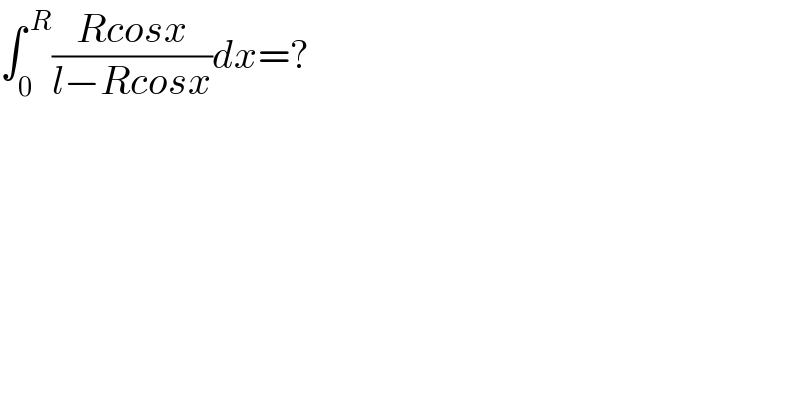
$$\int_{\mathrm{0}} ^{\:{R}} \frac{{Rcosx}}{{l}−{Rcosx}}{dx}=? \\ $$
Answered by Ar Brandon last updated on 11/Feb/23
![I=∫_0 ^R ((Rcosx)/(l−Rcosx))dx=∫_0 ^R ((l/(l−Rcosx))−1)dx =∫_0 ^(tan((R/2))) (l/(l−R((1−t^2 )/(1+t^2 ))))∙((2dt)/(1+t^2 ))−R =2l∫_0 ^(tan((R/2))) (dt/(l(1+t^2 )−R(1−t^2 )))−R =2l∫_0 ^(tan((R/2))) (dt/((R+l)t^2 +(l−R)))−R case1: l>R I=((2l)/( (√(l^2 −R^2 ))))[arctan(t(√((l+R)/(l−R))))]_0 ^(tan((R/2))) −R =((2l)/( (√(l^2 −R^2 ))))arctan(tan((R/2))(√((l+R)/(l−R))))−R case2: l<R I=(l/( (√(R^2 −l^2 ))))[ln∣((t(√(R+l))−(√(R−l)))/(t(√(R+l))+(√(R−l))))∣]_0 ^(tan((R/2))) −R](Q186857.png)
$${I}=\int_{\mathrm{0}} ^{{R}} \frac{{R}\mathrm{cos}{x}}{{l}−{R}\mathrm{cos}{x}}{dx}=\int_{\mathrm{0}} ^{{R}} \left(\frac{{l}}{{l}−{R}\mathrm{cos}{x}}−\mathrm{1}\right){dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{{R}}{\mathrm{2}}\right)} \frac{{l}}{{l}−{R}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\centerdot\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }−{R} \\ $$$$\:\:=\mathrm{2}{l}\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{{R}}{\mathrm{2}}\right)} \frac{{dt}}{{l}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)−{R}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}−{R} \\ $$$$\:\:=\mathrm{2}{l}\int_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{{R}}{\mathrm{2}}\right)} \frac{{dt}}{\left({R}+{l}\right){t}^{\mathrm{2}} +\left({l}−{R}\right)}−{R} \\ $$$$\mathrm{case1}:\:{l}>{R} \\ $$$${I}=\frac{\mathrm{2}{l}}{\:\sqrt{{l}^{\mathrm{2}} −{R}^{\mathrm{2}} }}\left[\mathrm{arctan}\left({t}\sqrt{\frac{{l}+{R}}{{l}−{R}}}\right)\right]_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{{R}}{\mathrm{2}}\right)} −{R} \\ $$$$\:\:=\frac{\mathrm{2}{l}}{\:\sqrt{{l}^{\mathrm{2}} −{R}^{\mathrm{2}} }}\mathrm{arctan}\left(\mathrm{tan}\left(\frac{{R}}{\mathrm{2}}\right)\sqrt{\frac{{l}+{R}}{{l}−{R}}}\right)−{R} \\ $$$$\mathrm{case2}:\:{l}<{R} \\ $$$${I}=\frac{{l}}{\:\sqrt{{R}^{\mathrm{2}} −{l}^{\mathrm{2}} }}\left[\mathrm{ln}\mid\frac{{t}\sqrt{{R}+{l}}−\sqrt{{R}−{l}}}{{t}\sqrt{{R}+{l}}+\sqrt{{R}−{l}}}\mid\right]_{\mathrm{0}} ^{\mathrm{tan}\left(\frac{{R}}{\mathrm{2}}\right)} −{R} \\ $$
Commented by liuxinnan last updated on 12/Feb/23

$${thanks}\:{you} \\ $$
