
Question Number 219870 by SdC355 last updated on 03/May/25

$$\int_{\mathrm{0}} ^{\:\infty} \:{K}_{\nu} \left({r}\right)\mathrm{d}{r} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:{t}\centerdot{Y}_{\mathrm{0}} \left({t}\right)\mathrm{d}{t} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:\:\frac{\mathrm{sin}\left({t}\right){e}^{−{kt}} }{{t}^{\mathrm{2}} +\rho^{\mathrm{2}} }\mathrm{d}{t}\: \\ $$
Answered by MrGaster last updated on 04/May/25
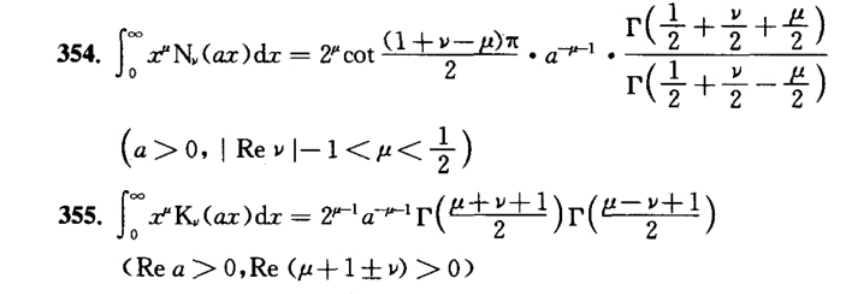
Commented by MrGaster last updated on 04/May/25
Just substitute the numerical value.
