
Question Number 111082 by john santu last updated on 02/Sep/20
![[∫_0 ^∞ JS dx ] ∫_0 ^(π/2) ((sin (x)(4+sin^2 (x)))/((4−sin^2 (x))^2 )) dx ?](Q111082.png)
$$\:\:\:\left[\int_{\mathrm{0}} ^{\infty} {JS}\:{dx}\:\right] \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{sin}\:\left({x}\right)\left(\mathrm{4}+\mathrm{sin}\:^{\mathrm{2}} \left({x}\right)\right)}{\left(\mathrm{4}−\mathrm{sin}\:^{\mathrm{2}} \left({x}\right)\right)^{\mathrm{2}} }\:{dx}\:? \\ $$
Commented by mathdave last updated on 02/Sep/20
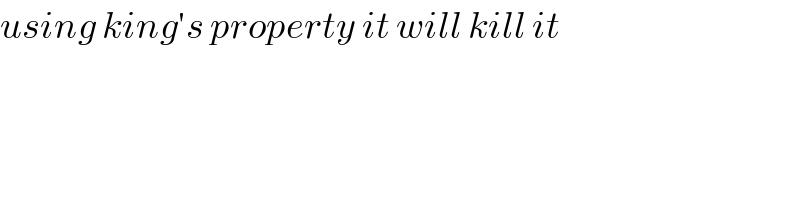
$${using}\:{king}'{s}\:{property}\:{it}\:{will}\:{kill}\:{it} \\ $$
Answered by Sarah85 last updated on 02/Sep/20
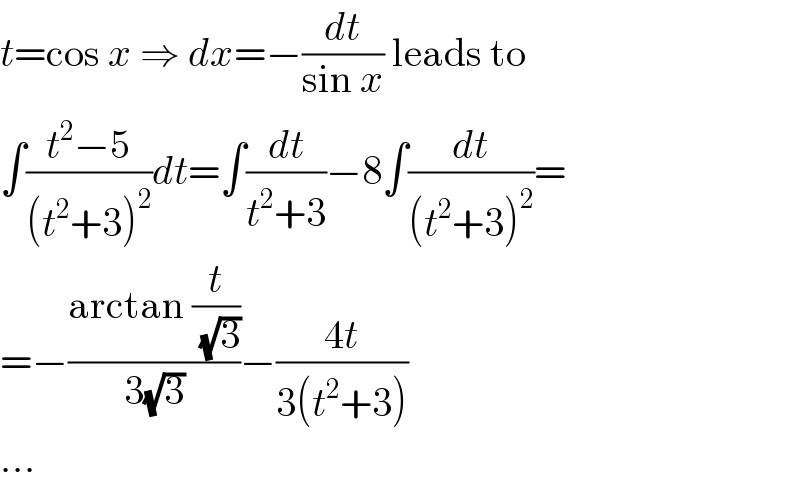
$${t}=\mathrm{cos}\:{x}\:\Rightarrow\:{dx}=−\frac{{dt}}{\mathrm{sin}\:{x}}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\int\frac{{t}^{\mathrm{2}} −\mathrm{5}}{\left({t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }{dt}=\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}}−\mathrm{8}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }= \\ $$$$=−\frac{\mathrm{arctan}\:\frac{{t}}{\:\sqrt{\mathrm{3}}}}{\mathrm{3}\sqrt{\mathrm{3}}}−\frac{\mathrm{4}{t}}{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{3}\right)} \\ $$$$... \\ $$
