
Question Number 211434 by Davidtim last updated on 09/Sep/24
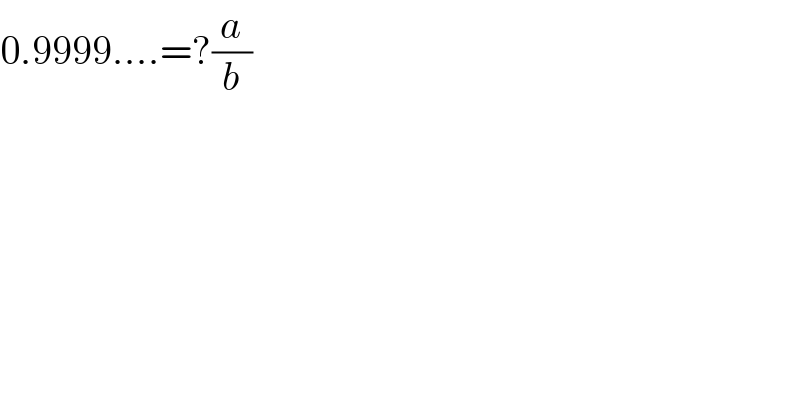
$$\mathrm{0}.\mathrm{9999}....=?\frac{{a}}{{b}} \\ $$
Answered by Rasheed.Sindhi last updated on 09/Sep/24

$${n}=\mathrm{0}.\mathrm{9999}.... \\ $$$$\mathrm{10}{n}=\mathrm{9}.\mathrm{9999} \\ $$$$\mathrm{10}{n}−{n}=\mathrm{9} \\ $$$${n}=\frac{\mathrm{9}}{\mathrm{9}}=\mathrm{1}=\frac{\mathrm{1}}{\mathrm{1}} \\ $$
Commented by Davidtim last updated on 09/Sep/24
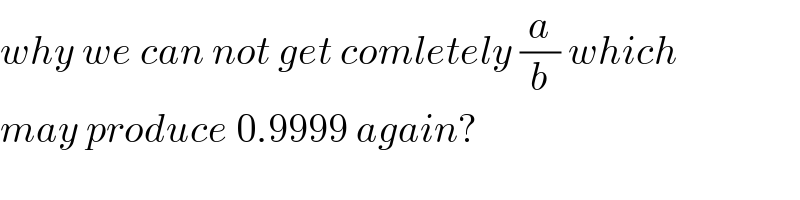
$${why}\:{we}\:{can}\:{not}\:{get}\:{comletely}\:\frac{{a}}{{b}}\:{which} \\ $$$${may}\:{produce}\:\mathrm{0}.\mathrm{9999}\:{again}? \\ $$
Commented by Frix last updated on 09/Sep/24
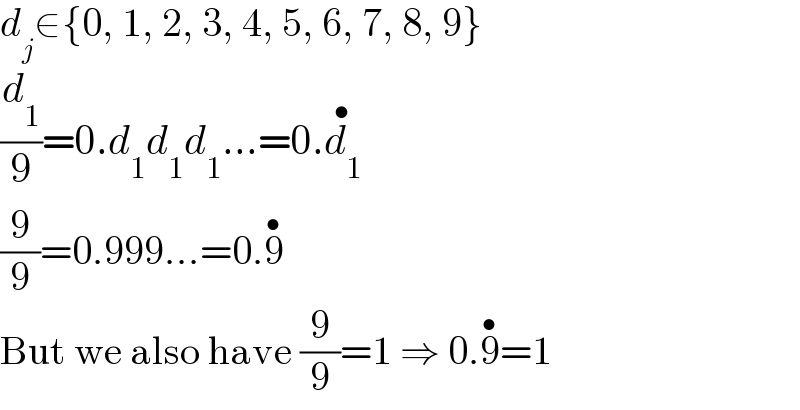
$${d}_{{j}} \in\left\{\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:\mathrm{6},\:\mathrm{7},\:\mathrm{8},\:\mathrm{9}\right\} \\ $$$$\frac{{d}_{\mathrm{1}} }{\mathrm{9}}=\mathrm{0}.{d}_{\mathrm{1}} {d}_{\mathrm{1}} {d}_{\mathrm{1}} ...=\mathrm{0}.\overset{\bullet} {{d}_{\mathrm{1}} } \\ $$$$\frac{\mathrm{9}}{\mathrm{9}}=\mathrm{0}.\mathrm{999}...=\mathrm{0}.\overset{\bullet} {\mathrm{9}} \\ $$$$\mathrm{But}\:\mathrm{we}\:\mathrm{also}\:\mathrm{have}\:\frac{\mathrm{9}}{\mathrm{9}}=\mathrm{1}\:\Rightarrow\:\mathrm{0}.\overset{\bullet} {\mathrm{9}}=\mathrm{1} \\ $$
