
Question Number 14747 by 433 last updated on 04/Jun/17
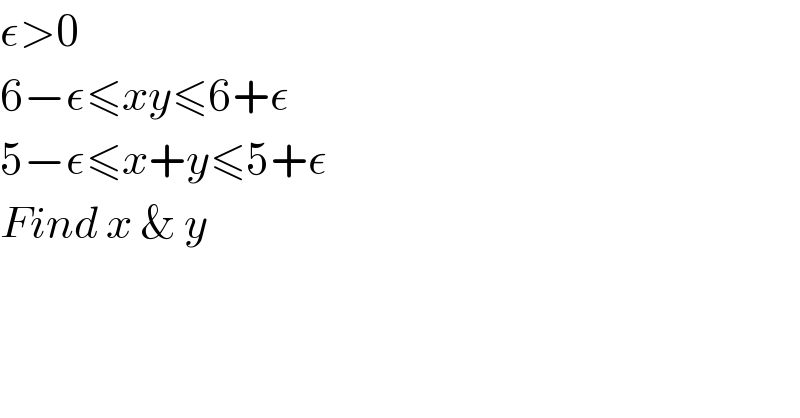
$$\epsilon>\mathrm{0} \\ $$ $$\mathrm{6}−\epsilon\leqslant{xy}\leqslant\mathrm{6}+\epsilon \\ $$ $$\mathrm{5}−\epsilon\leqslant{x}+{y}\leqslant\mathrm{5}+\epsilon \\ $$ $${Find}\:{x}\:\&\:{y} \\ $$
Answered by ajfour last updated on 04/Jun/17
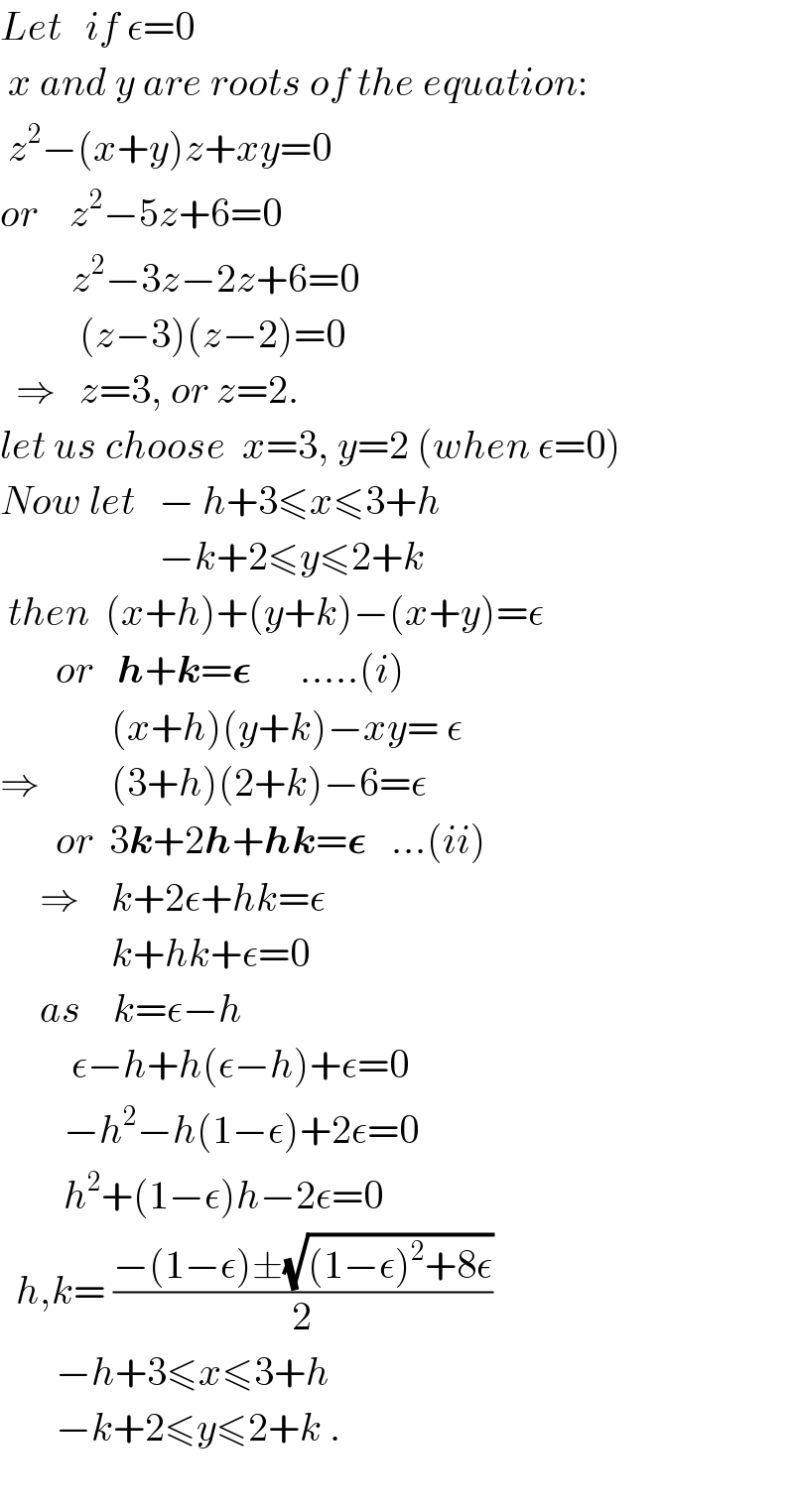
$${Let}\:\:\:{if}\:\epsilon=\mathrm{0} \\ $$ $$\:{x}\:{and}\:{y}\:{are}\:{roots}\:{of}\:{the}\:{equation}: \\ $$ $$\:{z}^{\mathrm{2}} −\left({x}+{y}\right){z}+{xy}=\mathrm{0} \\ $$ $${or}\:\:\:\:{z}^{\mathrm{2}} −\mathrm{5}{z}+\mathrm{6}=\mathrm{0} \\ $$ $$\:\:\:\:\:\:\:\:\:{z}^{\mathrm{2}} −\mathrm{3}{z}−\mathrm{2}{z}+\mathrm{6}=\mathrm{0} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\left({z}−\mathrm{3}\right)\left({z}−\mathrm{2}\right)=\mathrm{0} \\ $$ $$\:\:\Rightarrow\:\:\:{z}=\mathrm{3},\:{or}\:{z}=\mathrm{2}. \\ $$ $${let}\:{us}\:{choose}\:\:{x}=\mathrm{3},\:{y}=\mathrm{2}\:\left({when}\:\epsilon=\mathrm{0}\right) \\ $$ $${Now}\:{let}\:\:\:−\:{h}+\mathrm{3}\leqslant{x}\leqslant\mathrm{3}+{h} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{k}+\mathrm{2}\leqslant{y}\leqslant\mathrm{2}+{k} \\ $$ $$\:{then}\:\:\left({x}+{h}\right)+\left({y}+{k}\right)−\left({x}+{y}\right)=\epsilon \\ $$ $$\:\:\:\:\:\:\:{or}\:\:\:\boldsymbol{{h}}+\boldsymbol{{k}}=\boldsymbol{\epsilon}\:\:\:\:\:\:.....\left({i}\right) \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({x}+{h}\right)\left({y}+{k}\right)−{xy}=\:\epsilon \\ $$ $$\Rightarrow\:\:\:\:\:\:\:\:\:\left(\mathrm{3}+{h}\right)\left(\mathrm{2}+{k}\right)−\mathrm{6}=\epsilon \\ $$ $$\:\:\:\:\:\:\:{or}\:\:\mathrm{3}\boldsymbol{{k}}+\mathrm{2}\boldsymbol{{h}}+\boldsymbol{{hk}}=\boldsymbol{\epsilon}\:\:\:...\left({ii}\right) \\ $$ $$\:\:\:\:\:\Rightarrow\:\:\:\:{k}+\mathrm{2}\epsilon+{hk}=\epsilon \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{k}+{hk}+\epsilon=\mathrm{0} \\ $$ $$\:\:\:\:\:{as}\:\:\:\:{k}=\epsilon−{h} \\ $$ $$\:\:\:\:\:\:\:\:\:\epsilon−{h}+{h}\left(\epsilon−{h}\right)+\epsilon=\mathrm{0} \\ $$ $$\:\:\:\:\:\:\:\:−{h}^{\mathrm{2}} −{h}\left(\mathrm{1}−\epsilon\right)+\mathrm{2}\epsilon=\mathrm{0}\:\:\:\:\:\: \\ $$ $$\:\:\:\:\:\:\:\:{h}^{\mathrm{2}} +\left(\mathrm{1}−\epsilon\right){h}−\mathrm{2}\epsilon=\mathrm{0} \\ $$ $$\:\:{h},{k}=\:\frac{−\left(\mathrm{1}−\epsilon\right)\pm\sqrt{\left(\mathrm{1}−\epsilon\right)^{\mathrm{2}} +\mathrm{8}\epsilon}}{\mathrm{2}} \\ $$ $$\:\:\:\:\:\:\:−{h}+\mathrm{3}\leqslant{x}\leqslant\mathrm{3}+{h} \\ $$ $$\:\:\:\:\:\:\:−{k}+\mathrm{2}\leqslant{y}\leqslant\mathrm{2}+{k}\:. \\ $$ $$ \\ $$
Commented byajfour last updated on 04/Jun/17

$${there}\:{might}\:{be}\:{some}\:\boldsymbol{\epsilon}{rror}.. \\ $$ $${someone}\:{please}\:{confirm}.. \\ $$
Commented bymrW1 last updated on 04/Jun/17
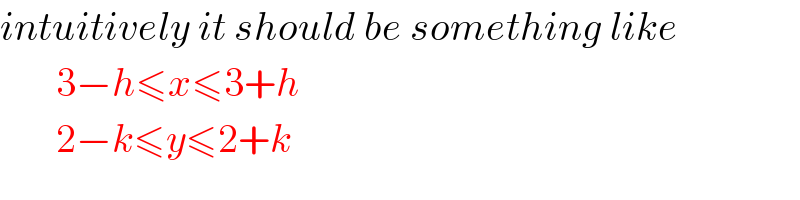
$${intuitively}\:{it}\:{should}\:{be}\:{something}\:{like} \\ $$ $$\:\:\:\:\:\:\:\mathrm{3}−{h}\leqslant{x}\leqslant\mathrm{3}+{h} \\ $$ $$\:\:\:\:\:\:\:\mathrm{2}−{k}\leqslant{y}\leqslant\mathrm{2}+{k} \\ $$
Commented byajfour last updated on 04/Jun/17

$${thank}\:{you}\:{sir},\:{God}\:{bless}\:{you}\:{sir}. \\ $$ $${but}\:{then}\:{the}\:\boldsymbol{\epsilon}{rror}\:\:{had}\:{to}\:{be}\:{there}. \\ $$
