
Question Number 141859 by iloveisrael last updated on 24/May/21
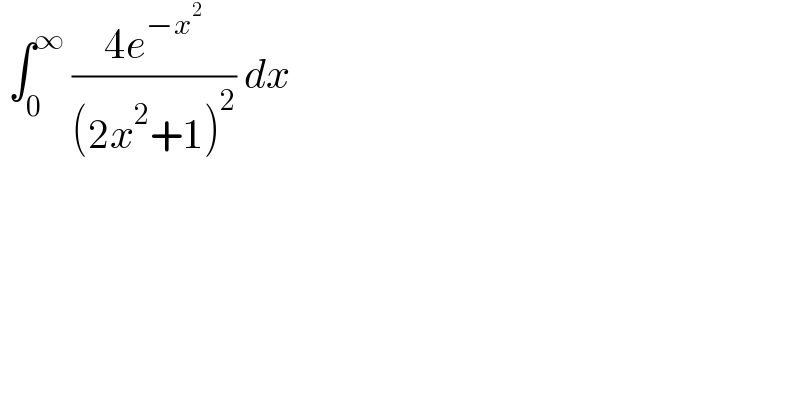
$$\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{4}{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\: \\ $$
Commented by Dwaipayan Shikari last updated on 24/May/21

$$\sqrt{\pi} \\ $$
Answered by qaz last updated on 24/May/21

$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{4}{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } \frac{\mathrm{1}}{\Gamma\left(\mathrm{2}\right)}\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)} {dudx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}} {du}\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {e}^{−\mathrm{2}{ux}^{\mathrm{2}} } {dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}} {du}\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{2}{u}+\mathrm{1}\right){x}^{\mathrm{2}} } {dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\infty} {ue}^{−{u}} \frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\left(\mathrm{2}{u}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{du} \\ $$$$=\sqrt{\pi}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{ue}^{−{u}} }{\:\sqrt{\mathrm{2}{u}+\mathrm{1}}}{du} \\ $$$$=−\sqrt{\pi}\frac{\sqrt{\mathrm{2}{u}+\mathrm{1}}}{{e}^{{u}} }\mid_{\mathrm{0}} ^{\infty} \\ $$$$=\sqrt{\pi} \\ $$
Commented by qaz last updated on 24/May/21
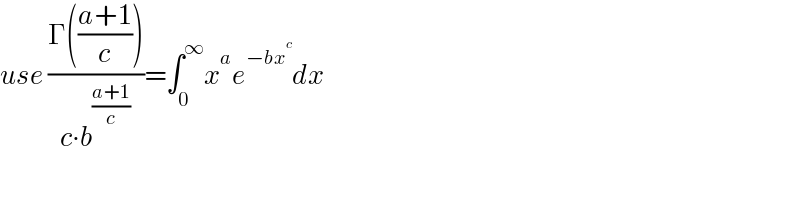
$${use}\:\frac{\Gamma\left(\frac{{a}+\mathrm{1}}{{c}}\right)}{{c}\centerdot{b}^{\frac{{a}+\mathrm{1}}{{c}}} }=\int_{\mathrm{0}} ^{\infty} {x}^{{a}} {e}^{−{bx}^{{c}} } {dx} \\ $$
Commented by Dwaipayan Shikari last updated on 24/May/21
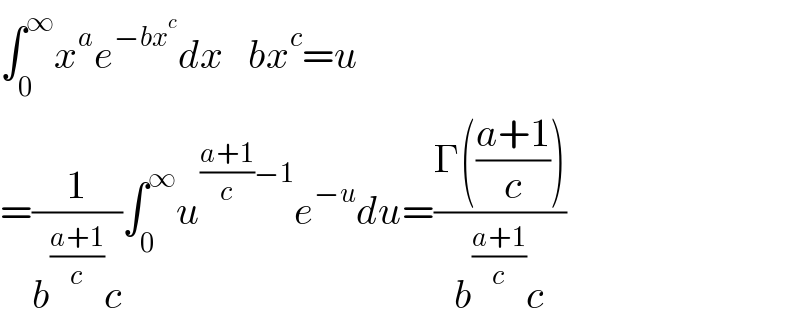
$$\int_{\mathrm{0}} ^{\infty} {x}^{{a}} {e}^{−{bx}^{{c}} } {dx}\:\:\:{bx}^{{c}} ={u} \\ $$$$=\frac{\mathrm{1}}{{b}^{\frac{{a}+\mathrm{1}}{{c}}} {c}}\int_{\mathrm{0}} ^{\infty} {u}^{\frac{{a}+\mathrm{1}}{{c}}−\mathrm{1}} {e}^{−{u}} {du}=\frac{\Gamma\left(\frac{{a}+\mathrm{1}}{{c}}\right)}{{b}^{\frac{{a}+\mathrm{1}}{{c}}} {c}} \\ $$
Answered by mindispower last updated on 24/May/21
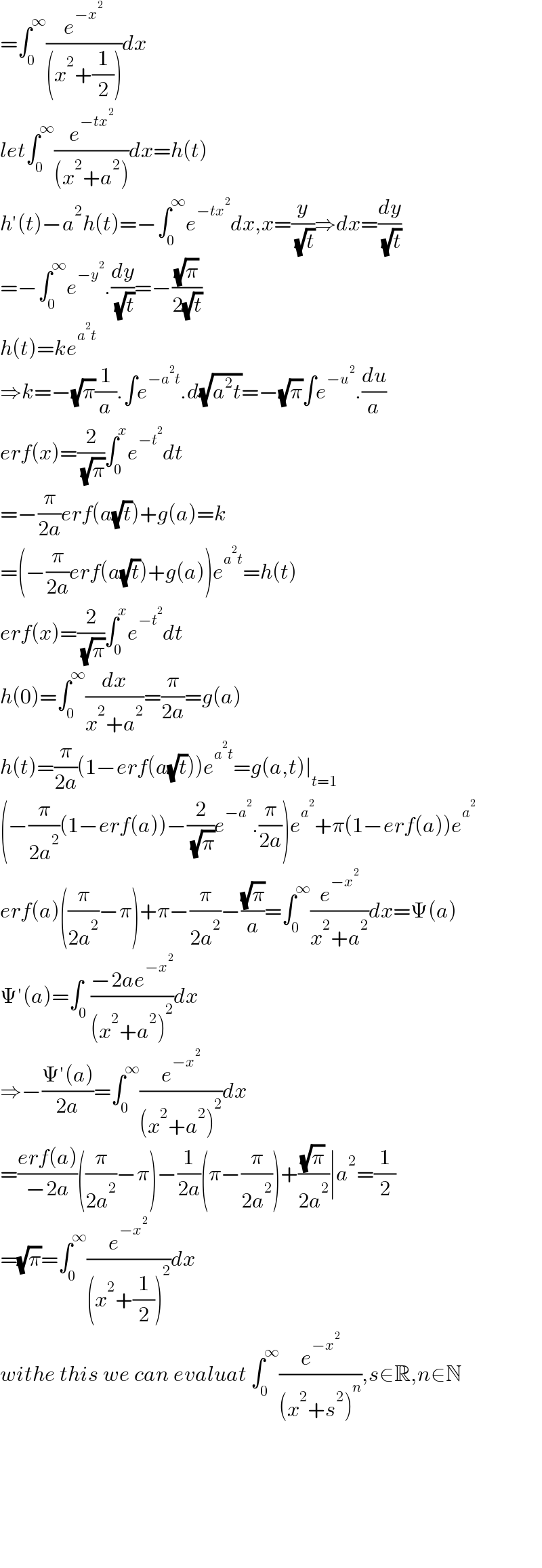
$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)}{dx} \\ $$$${let}\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{tx}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{dx}={h}\left({t}\right) \\ $$$${h}'\left({t}\right)−{a}^{\mathrm{2}} {h}\left({t}\right)=−\int_{\mathrm{0}} ^{\infty} {e}^{−{tx}^{\mathrm{2}} } {dx},{x}=\frac{{y}}{\:\sqrt{{t}}}\Rightarrow{dx}=\frac{{dy}}{\:\sqrt{{t}}} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} {e}^{−{y}^{\mathrm{2}} } .\frac{{dy}}{\:\sqrt{{t}}}=−\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{{t}}} \\ $$$${h}\left({t}\right)={ke}^{{a}^{\mathrm{2}} {t}} \\ $$$$\Rightarrow{k}=−\sqrt{\pi}\frac{\mathrm{1}}{{a}}.\int{e}^{−{a}^{\mathrm{2}} {t}} .{d}\sqrt{{a}^{\mathrm{2}} {t}}=−\sqrt{\pi}\int{e}^{−{u}^{\mathrm{2}} } .\frac{{du}}{{a}} \\ $$$${erf}\left({x}\right)=\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{{x}} {e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$$=−\frac{\pi}{\mathrm{2}{a}}{erf}\left({a}\sqrt{{t}}\right)+{g}\left({a}\right)={k} \\ $$$$=\left(−\frac{\pi}{\mathrm{2}{a}}{erf}\left({a}\sqrt{{t}}\right)+{g}\left({a}\right)\right){e}^{{a}^{\mathrm{2}} {t}} ={h}\left({t}\right) \\ $$$${erf}\left({x}\right)=\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{{x}} {e}^{−{t}^{\mathrm{2}} } {dt} \\ $$$${h}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}{a}}={g}\left({a}\right) \\ $$$${h}\left({t}\right)=\frac{\pi}{\mathrm{2}{a}}\left(\mathrm{1}−{erf}\left({a}\sqrt{{t}}\right)\right){e}^{{a}^{\mathrm{2}} {t}} ={g}\left({a},{t}\right)\mid_{{t}=\mathrm{1}} \\ $$$$\left(−\frac{\pi}{\mathrm{2}{a}^{\mathrm{2}} }\left(\mathrm{1}−{erf}\left({a}\right)\right)−\frac{\mathrm{2}}{\:\sqrt{\pi}}{e}^{−{a}^{\mathrm{2}} } .\frac{\pi}{\mathrm{2}{a}}\right){e}^{{a}^{\mathrm{2}} } +\pi\left(\mathrm{1}−{erf}\left({a}\right)\right){e}^{{a}^{\mathrm{2}} } \\ $$$${erf}\left({a}\right)\left(\frac{\pi}{\mathrm{2}{a}^{\mathrm{2}} }−\pi\right)+\pi−\frac{\pi}{\mathrm{2}{a}^{\mathrm{2}} }−\frac{\sqrt{\pi}}{{a}}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}=\Psi\left({a}\right) \\ $$$$\Psi'\left({a}\right)=\int_{\mathrm{0}} \frac{−\mathrm{2}{ae}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow−\frac{\Psi'\left({a}\right)}{\mathrm{2}{a}}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$$=\frac{{erf}\left({a}\right)}{−\mathrm{2}{a}}\left(\frac{\pi}{\mathrm{2}{a}^{\mathrm{2}} }−\pi\right)−\frac{\mathrm{1}}{\mathrm{2}{a}}\left(\pi−\frac{\pi}{\mathrm{2}{a}^{\mathrm{2}} }\right)+\frac{\sqrt{\pi}}{\mathrm{2}{a}^{\mathrm{2}} }\mid{a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\sqrt{\pi}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx} \\ $$$${withe}\:{this}\:{we}\:{can}\:{evaluat}\:\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} +{s}^{\mathrm{2}} \right)^{{n}} },{s}\in\mathbb{R},{n}\in\mathbb{N} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
