
Question Number 218907 by malwan last updated on 17/Apr/25
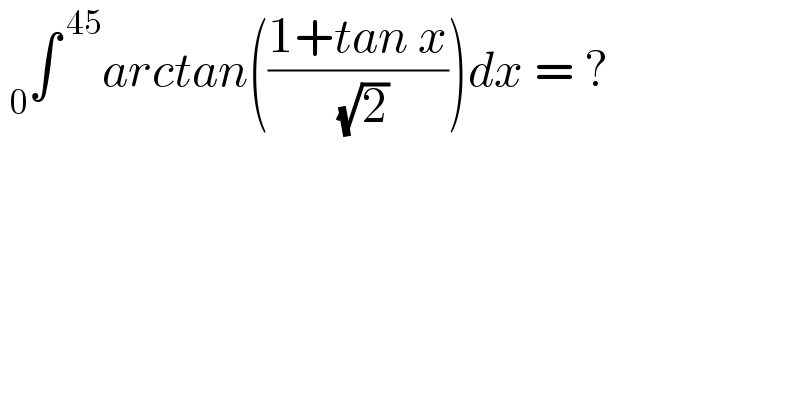
$$\:_{\mathrm{0}} \int^{\:\mathrm{45}} {arctan}\left(\frac{\mathrm{1}+{tan}\:{x}}{\:\sqrt{\mathrm{2}}}\right){dx}\:=\:? \\ $$
Commented by mr W last updated on 17/Apr/25

$${you}\:{should}\:{make}\:{clear}\:{what}\:{you} \\ $$$${mean}\:{with}\:\int_{\mathrm{0}} ^{\mathrm{45}} \ast.\:{maybe}\:{you}\:{mean} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \ast,\:{then}\:{you}\:{should}\:{also}\:{write} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \ast.\:{otherwise}\:{the}\:{integral}\:{is}\:{not} \\ $$$${defined}. \\ $$
Commented by malwan last updated on 17/Apr/25
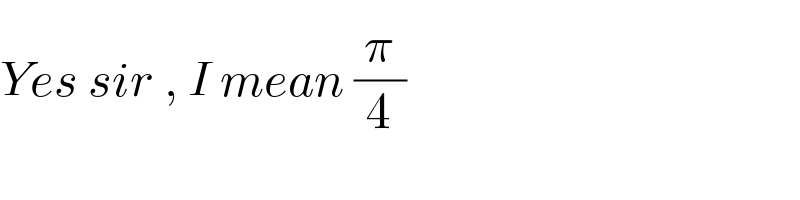
$${Yes}\:{sir}\:,\:{I}\:{mean}\:\frac{\pi}{\mathrm{4}}\:\:\cancel{\lesseqgtr} \\ $$
Answered by Nicholas666 last updated on 17/Apr/25

$$\:\:\:\:\:\:\:\frac{\mathrm{45}\pi}{\mathrm{8}}\: \\ $$
Commented by malwan last updated on 17/Apr/25
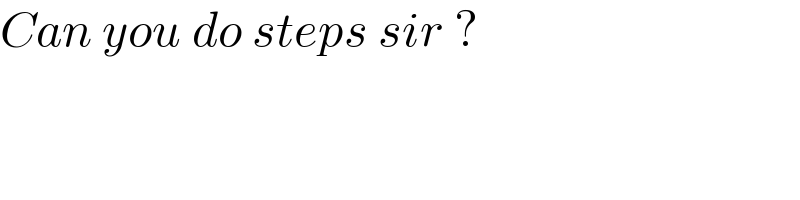
$${Can}\:{you}\:{do}\:{steps}\:{sir}\:?\:\cancel{\lesseqgtr} \\ $$
Commented by Nicholas666 last updated on 17/Apr/25
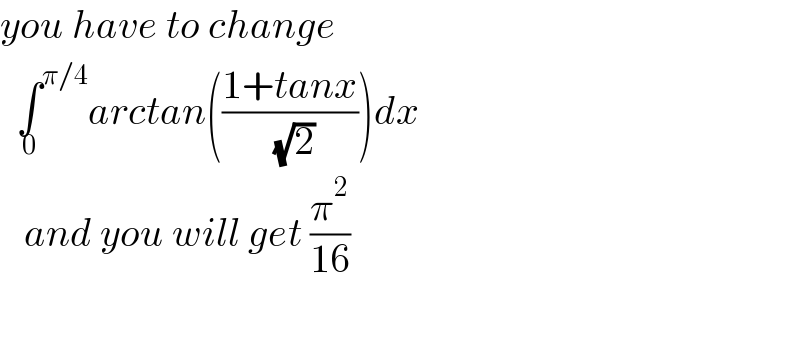
$${you}\:{have}\:{to}\:{change}\: \\ $$$$\:\:\underset{\mathrm{0}} {\int}^{\pi/\mathrm{4}} {arctan}\left(\frac{\mathrm{1}+{tanx}}{\:\sqrt{\mathrm{2}}}\right){dx} \\ $$$$\:\:\:{and}\:{you}\:{will}\:{get}\:\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\: \\ $$$$ \\ $$
Commented by Nicholas666 last updated on 17/Apr/25

$$\left({using}\:{radians}\right){we}\:{want}\:{to}\:{evaluate}\:{definite}\:{integral} \\ $$$$\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {arctan}\left(\frac{\mathrm{1}+{tanx}}{\:\sqrt{\mathrm{2}}}\right){dx} \\ $$$${using}\:{the}\:{interval}\:{invertin}\:{subtitution} \\ $$$${where}\:{we}\:{raplace}\:{x}\:{with}\:\frac{\pi}{\mathrm{4}}−{x},\:{wi}\:{find}\:{the}\:{sum}\:{of} \\ $$$${angles}\:{identity}\:{for}\:{tanget}\:{that}\: \\ $$$${tan}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)=\frac{{tan}\frac{\pi}{\mathrm{4}}−{tan}\:{x}}{\mathrm{1}+{tan}\frac{\pi}{\mathrm{4}}{tan}\:{x}}=\frac{\mathrm{1}−{tanx}}{\mathrm{1}+{tanx}}, \\ $$$${I}=\int_{\pi/\mathrm{4}} ^{\mathrm{0}} {arctan}\left(\frac{\mathrm{1}+\frac{\mathrm{1}−{tan}\:{x}}{\mathrm{1}+{tan}\:{x}}}{\:\sqrt{\mathrm{2}}}.\left(−{dx}\right)\right. \\ $$$$\:=\int_{\mathrm{0}} ^{\pi/\mathrm{4}} {arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{1}+{tan}\:{x}}\right){dx} \\ $$$$\:=\int_{\mathrm{0}\:} ^{\pi/\mathrm{4}} {arcot}\:\left(\frac{\mathrm{1}+{tan}\:{x}}{\:\sqrt{\mathrm{2}}}\right){dx}\:\:,{since}\:{x}>\mathrm{0} \\ $$$$ \\ $$$$\:\:\:{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \left({arctan}\left(\frac{\mathrm{1}+{tan}\:{x}}{\:\sqrt{\mathrm{2}}}\right)+{arcot}\left(\frac{\mathrm{1}+{tan}\:{x}}{\:\sqrt{\mathrm{2}}}\right)\right){dx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{4}} \frac{\pi}{\mathrm{2}}{dx}\: \\ $$$$\:\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$$$ \\ $$
