
Question Number 195674 by Rodier97 last updated on 07/Aug/23
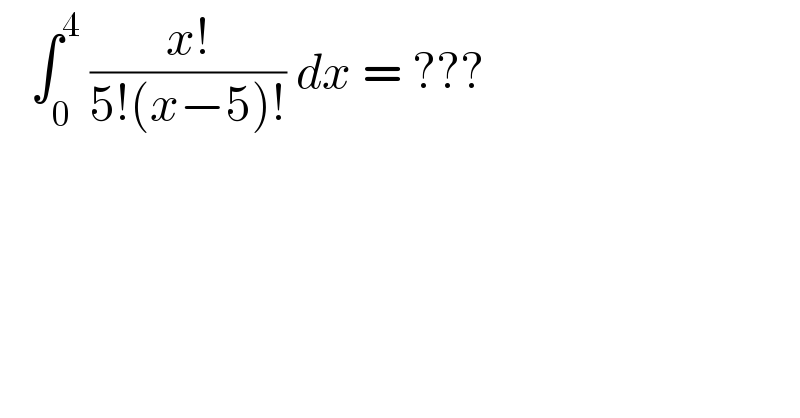
$$\:\:\:\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{{x}!}{\mathrm{5}!\left({x}−\mathrm{5}\right)!}\:{dx}\:=\:??? \\ $$
Commented by mr W last updated on 07/Aug/23
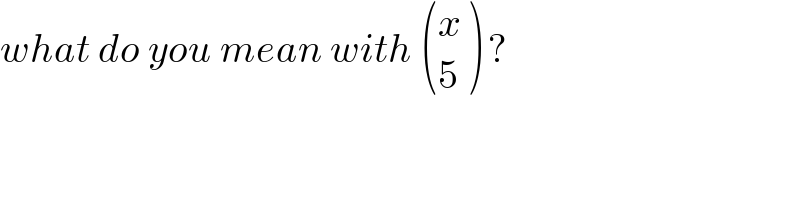
$${what}\:{do}\:{you}\:{mean}\:{with}\:\begin{pmatrix}{{x}}\\{\mathrm{5}}\end{pmatrix}\:? \\ $$
Commented by Rodier97 last updated on 07/Aug/23

$$ \\ $$$$\:\:\:\:{C}_{{x}} ^{\:\mathrm{5}} =\frac{{x}!}{\mathrm{5}!\left({x}−\mathrm{5}\right)!} \\ $$
Commented by mr W last updated on 07/Aug/23
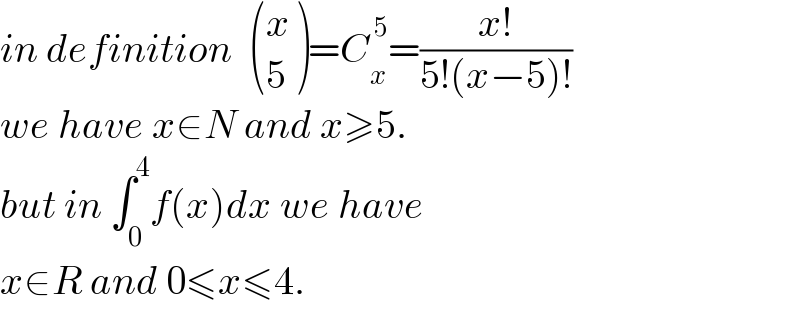
$${in}\:{definition}\:\:\begin{pmatrix}{{x}}\\{\mathrm{5}}\end{pmatrix}={C}_{{x}} ^{\:\mathrm{5}} =\frac{{x}!}{\mathrm{5}!\left({x}−\mathrm{5}\right)!}\: \\ $$$${we}\:{have}\:{x}\in{N}\:{and}\:{x}\geqslant\mathrm{5}. \\ $$$${but}\:{in}\:\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}\right){dx}\:{we}\:{have}\: \\ $$$${x}\in{R}\:{and}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{4}. \\ $$
Commented by kapoorshah last updated on 07/Aug/23
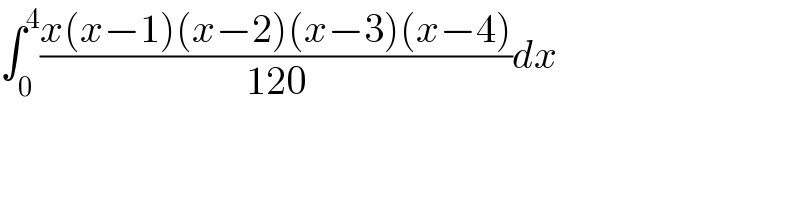
$$\int_{\mathrm{0}} ^{\mathrm{4}} \frac{{x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}{\mathrm{120}}{dx} \\ $$
