
Question Number 4559 by love math last updated on 07/Feb/16
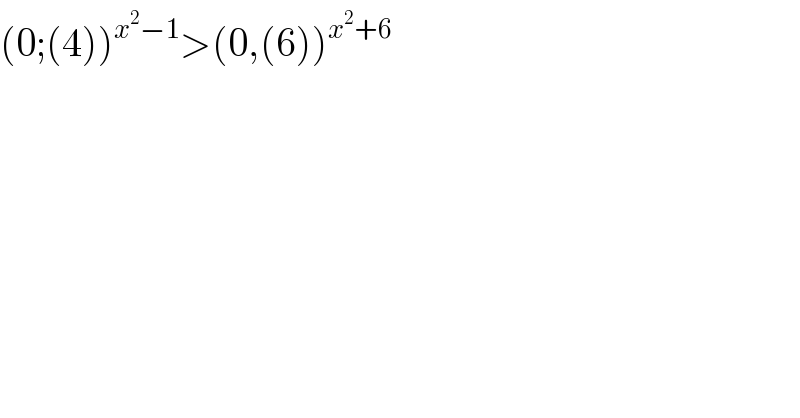
$$\left(\mathrm{0};\left(\mathrm{4}\right)\right)^{{x}^{\mathrm{2}} −\mathrm{1}} >\left(\mathrm{0},\left(\mathrm{6}\right)\right)^{{x}^{\mathrm{2}} +\mathrm{6}} \\ $$
Commented byYozzii last updated on 07/Feb/16
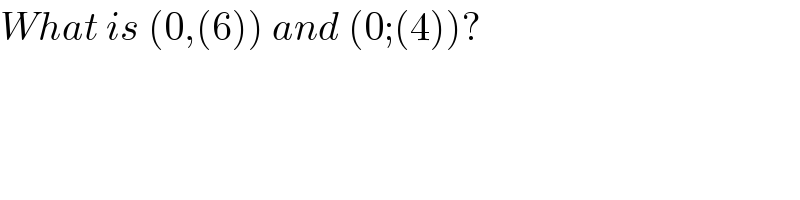
$${What}\:{is}\:\left(\mathrm{0},\left(\mathrm{6}\right)\right)\:{and}\:\left(\mathrm{0};\left(\mathrm{4}\right)\right)? \\ $$
Commented byYozzii last updated on 07/Feb/16
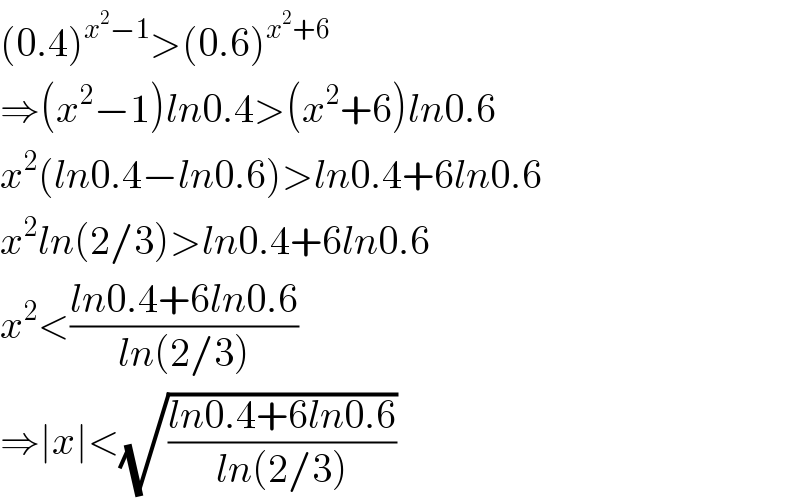
$$\left(\mathrm{0}.\mathrm{4}\right)^{{x}^{\mathrm{2}} −\mathrm{1}} >\left(\mathrm{0}.\mathrm{6}\right)^{{x}^{\mathrm{2}} +\mathrm{6}} \\ $$ $$\Rightarrow\left({x}^{\mathrm{2}} −\mathrm{1}\right){ln}\mathrm{0}.\mathrm{4}>\left({x}^{\mathrm{2}} +\mathrm{6}\right){ln}\mathrm{0}.\mathrm{6} \\ $$ $${x}^{\mathrm{2}} \left({ln}\mathrm{0}.\mathrm{4}−{ln}\mathrm{0}.\mathrm{6}\right)>{ln}\mathrm{0}.\mathrm{4}+\mathrm{6}{ln}\mathrm{0}.\mathrm{6} \\ $$ $${x}^{\mathrm{2}} {ln}\left(\mathrm{2}/\mathrm{3}\right)>{ln}\mathrm{0}.\mathrm{4}+\mathrm{6}{ln}\mathrm{0}.\mathrm{6} \\ $$ $${x}^{\mathrm{2}} <\frac{{ln}\mathrm{0}.\mathrm{4}+\mathrm{6}{ln}\mathrm{0}.\mathrm{6}}{{ln}\left(\mathrm{2}/\mathrm{3}\right)}\: \\ $$ $$\Rightarrow\mid{x}\mid<\sqrt{\frac{{ln}\mathrm{0}.\mathrm{4}+\mathrm{6}{ln}\mathrm{0}.\mathrm{6}}{{ln}\left(\mathrm{2}/\mathrm{3}\right)}} \\ $$
