
Question Number 192668 by mathocean1 last updated on 24/May/23
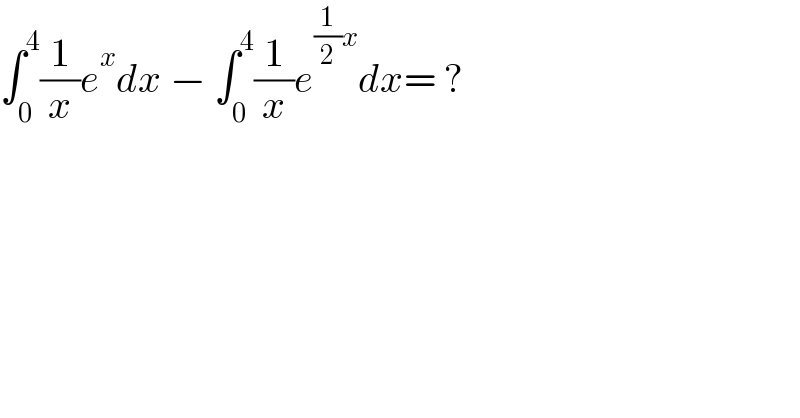
$$\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{1}}{{x}}{e}^{{x}} {dx}\:−\:\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{1}}{{x}}{e}^{\frac{\mathrm{1}}{\mathrm{2}}{x}} {dx}=\:? \\ $$
Answered by witcher3 last updated on 24/May/23
![fals ∫_0 ^1 (e^(kx) /x)dx not rieman integrabl but lesbegue integrable cause ∀n∈Z_+ μ([0,(1/n)])=(1/n)→0for n→∞ ∀n∈N ∫_(1/n) ^4 (e^x /x)dx=∫_0 ^4 (e^x /x)1_([(1/n),4]) ..exist for all n∈N](Q192671.png)
$$\mathrm{fals} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{e}^{\mathrm{kx}} }{\mathrm{x}}\mathrm{dx}\:\mathrm{not}\:\mathrm{rieman}\:\mathrm{integrabl}\:\mathrm{but}\:\mathrm{lesbegue}\:\mathrm{integrable} \\ $$$$\mathrm{cause}\:\forall\mathrm{n}\in\mathbb{Z}_{+} \mu\left(\left[\mathrm{0},\frac{\mathrm{1}}{\mathrm{n}}\right]\right)=\frac{\mathrm{1}}{\mathrm{n}}\rightarrow\mathrm{0for}\:\mathrm{n}\rightarrow\infty \\ $$$$\forall\mathrm{n}\in\mathbb{N} \\ $$$$\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{\mathrm{4}} \frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{x}}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{x}}\mathrm{1}_{\left[\frac{\mathrm{1}}{\mathrm{n}},\mathrm{4}\right]} ..\mathrm{exist}\:\mathrm{for}\:\mathrm{all}\:\mathrm{n}\in\mathbb{N} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Frix last updated on 24/May/23

$$\int\frac{\mathrm{e}^{{x}} }{{x}}{dx}=\mathrm{Ei}\:\left({x}\right)\:+{C} \\ $$$$\int\frac{{e}^{\frac{{x}}{\mathrm{2}}} }{{x}}{dx}=\mathrm{Ei}\:\left(\frac{{x}}{\mathrm{2}}\right)\:+{C} \\ $$$$\mathrm{You}\:\mathrm{need}\:\mathrm{to}\:\mathrm{find}\:\mathrm{a}\:\mathrm{table}\:\mathrm{for}\:\mathrm{values}\:\mathrm{of}\:\mathrm{Ei}\:\left({x}\right) \\ $$$$\mathrm{The}\:\mathrm{answer}\:\mathrm{is}\:\approx.\mathrm{747750730933} \\ $$
Commented by mathocean1 last updated on 25/May/23

$${ok}\:{thanks} \\ $$
