
Question Number 189769 by mathocean1 last updated on 21/Mar/23
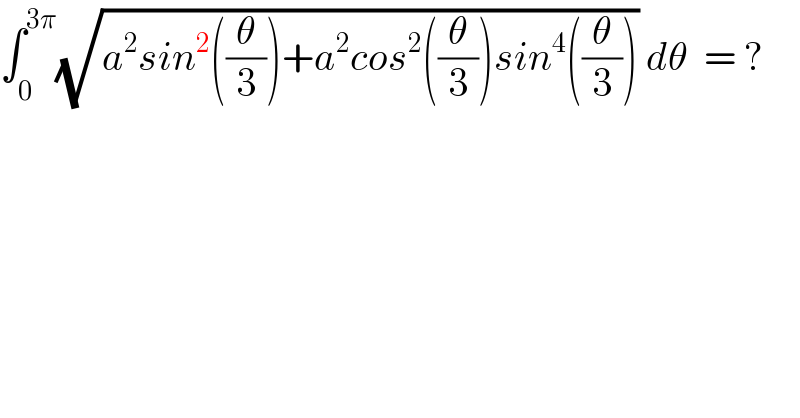
$$\int_{\mathrm{0}} ^{\mathrm{3}\pi} \sqrt{{a}^{\mathrm{2}} {sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{3}}\right)+{a}^{\mathrm{2}} {cos}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{3}}\right){sin}^{\mathrm{4}} \left(\frac{\theta}{\mathrm{3}}\right)}\:{d}\theta\:\:=\:? \\ $$
Commented by MJS_new last updated on 22/Mar/23
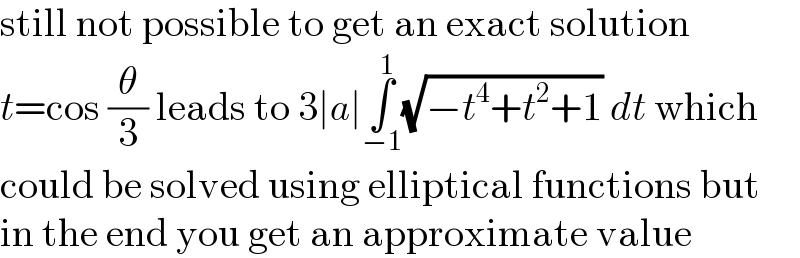
$$\mathrm{still}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{get}\:\mathrm{an}\:\mathrm{exact}\:\mathrm{solution} \\ $$$${t}=\mathrm{cos}\:\frac{\theta}{\mathrm{3}}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{3}\mid{a}\mid\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\sqrt{−{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}}\:{dt}\:\mathrm{which} \\ $$$$\mathrm{could}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{using}\:\mathrm{elliptical}\:\mathrm{functions}\:\mathrm{but} \\ $$$$\mathrm{in}\:\mathrm{the}\:\mathrm{end}\:\mathrm{you}\:\mathrm{get}\:\mathrm{an}\:\mathrm{approximate}\:\mathrm{value} \\ $$
Commented by mathocean1 last updated on 26/Mar/23

$${ok}\:{thanks} \\ $$
