Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 220896 by Nicholas666 last updated on 20/May/25

∫∫∫_( [0,∞]^( 3) ) ((x^2 y^2 z^2 )/((1 + x^2 + y^2 + z^2 )^5 )) dxdydz

$$ \\ $$$$\:\:\:\int\int\int_{\:\left[\mathrm{0},\infty\right]^{\:\mathrm{3}} } \frac{{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}^{\mathrm{2}} }{\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:+\:{z}^{\mathrm{2}} \right)^{\mathrm{5}} }\:{dxdydz}\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$

Answered by deleted50 last updated on 21/May/25

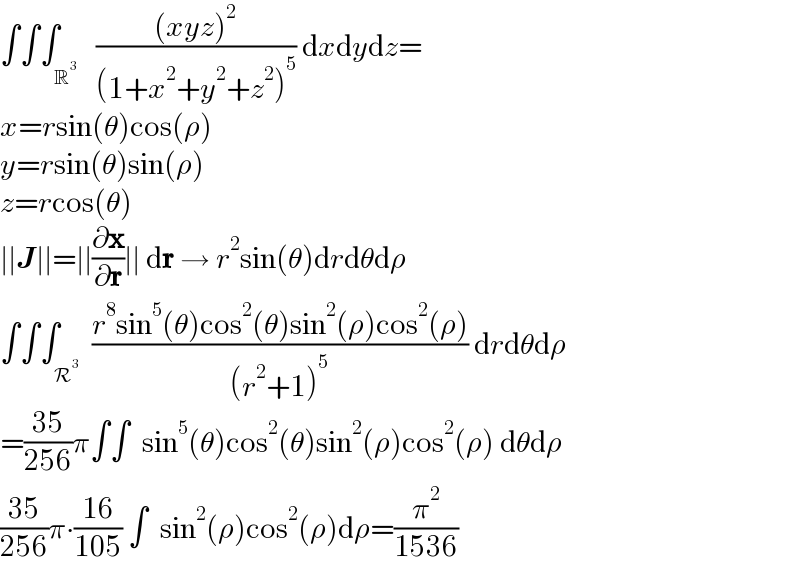
∫∫∫_R^3 (((xyz)^2 )/((1+x^2 +y^2 +z^2 )^5 )) dxdydz= x=rsin(θ)cos(ρ) y=rsin(θ)sin(ρ) z=rcos(θ) ∣∣J∣∣=∣∣(∂x/∂r)∣∣ dr → r^2 sin(θ)drdθdρ ∫∫∫_R^3 ((r^8 sin^5 (θ)cos^2 (θ)sin^2 (ρ)cos^2 (ρ))/((r^2 +1)^5 )) drdθdρ =((35)/(256))π∫∫ sin^5 (θ)cos^2 (θ)sin^2 (ρ)cos^2 (ρ) dθdρ ((35)/(256))π∙((16)/(105)) ∫ sin^2 (ρ)cos^2 (ρ)dρ=(π^2 /(1536))

$$\int\int\int_{\mathbb{R}^{\mathrm{3}} } \:\:\frac{\left({xyz}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{5}} }\:\mathrm{d}{x}\mathrm{d}{y}\mathrm{d}{z}= \\ $$$${x}={r}\mathrm{sin}\left(\theta\right)\mathrm{cos}\left(\rho\right) \\ $$$${y}={r}\mathrm{sin}\left(\theta\right)\mathrm{sin}\left(\rho\right) \\ $$$${z}={r}\mathrm{cos}\left(\theta\right) \\ $$$$\mid\mid\boldsymbol{{J}}\mid\mid=\mid\mid\frac{\partial\boldsymbol{\mathrm{x}}}{\partial\boldsymbol{\mathrm{r}}}\mid\mid\:\mathrm{d}\boldsymbol{\mathrm{r}}\:\rightarrow\:{r}^{\mathrm{2}} \mathrm{sin}\left(\theta\right)\mathrm{d}{r}\mathrm{d}\theta\mathrm{d}\rho \\ $$$$\int\int\int_{\mathcal{R}^{\mathrm{3}} } \:\frac{{r}^{\mathrm{8}} \mathrm{sin}^{\mathrm{5}} \left(\theta\right)\mathrm{cos}^{\mathrm{2}} \left(\theta\right)\mathrm{sin}^{\mathrm{2}} \left(\rho\right)\mathrm{cos}^{\mathrm{2}} \left(\rho\right)}{\left({r}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} }\:\mathrm{d}{r}\mathrm{d}\theta\mathrm{d}\rho \\ $$$$=\frac{\mathrm{35}}{\mathrm{256}}\pi\int\int\:\:\mathrm{sin}^{\mathrm{5}} \left(\theta\right)\mathrm{cos}^{\mathrm{2}} \left(\theta\right)\mathrm{sin}^{\mathrm{2}} \left(\rho\right)\mathrm{cos}^{\mathrm{2}} \left(\rho\right)\:\mathrm{d}\theta\mathrm{d}\rho \\ $$$$\frac{\mathrm{35}}{\mathrm{256}}\pi\centerdot\frac{\mathrm{16}}{\mathrm{105}}\:\int\:\:\mathrm{sin}^{\mathrm{2}} \left(\rho\right)\mathrm{cos}^{\mathrm{2}} \left(\rho\right)\mathrm{d}\rho=\frac{\pi^{\mathrm{2}} }{\mathrm{1536}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com