
Question Number 61785 by aliesam last updated on 08/Jun/19
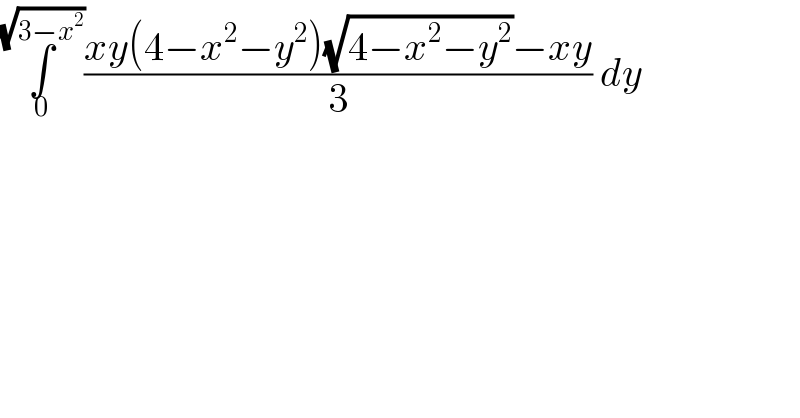
$$\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{3}−{x}^{\mathrm{2}} }} {\int}}\frac{{xy}\left(\mathrm{4}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }−{xy}}{\mathrm{3}}\:{dy} \\ $$
Answered by MJS last updated on 09/Jun/19
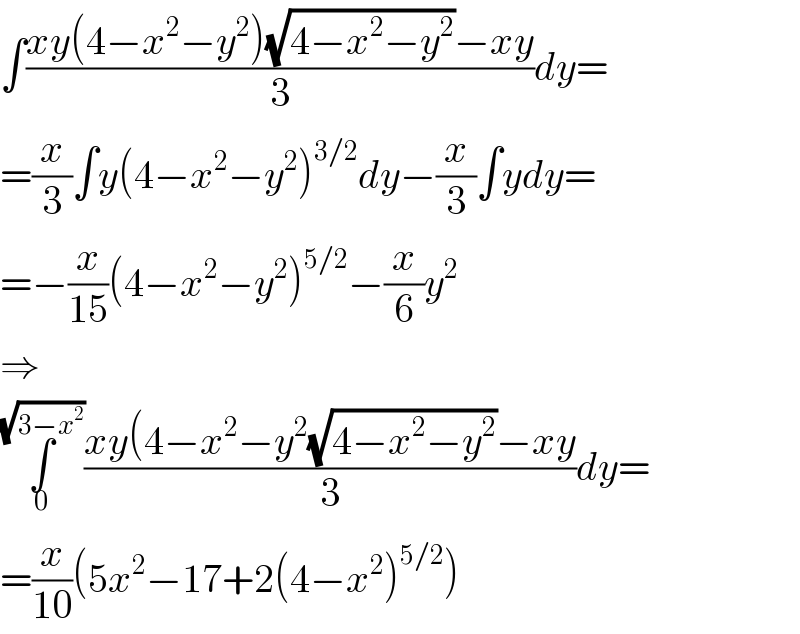
$$\int\frac{{xy}\left(\mathrm{4}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }−{xy}}{\mathrm{3}}{dy}= \\ $$$$=\frac{{x}}{\mathrm{3}}\int{y}\left(\mathrm{4}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} {dy}−\frac{{x}}{\mathrm{3}}\int{ydy}= \\ $$$$=−\frac{{x}}{\mathrm{15}}\left(\mathrm{4}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} −\frac{{x}}{\mathrm{6}}{y}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\sqrt{\mathrm{3}−{x}^{\mathrm{2}} }} {\int}}\frac{{xy}\left(\mathrm{4}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }−{xy}\right.}{\mathrm{3}}{dy}= \\ $$$$=\frac{{x}}{\mathrm{10}}\left(\mathrm{5}{x}^{\mathrm{2}} −\mathrm{17}+\mathrm{2}\left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} \right) \\ $$
Commented by aliesam last updated on 08/Jun/19

$${thanks}\:{sir} \\ $$
Commented by Prithwish sen last updated on 09/Jun/19
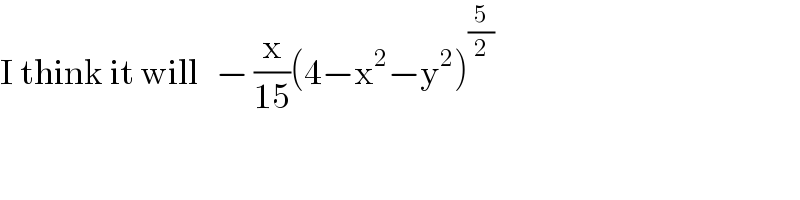
$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{will}\:\:\:−\:\frac{\mathrm{x}}{\mathrm{15}}\left(\mathrm{4}−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)^{\frac{\mathrm{5}}{\mathrm{2}}} \\ $$
Commented by MJS last updated on 09/Jun/19

$$\mathrm{you}'\mathrm{re}\:\mathrm{right},\:\mathrm{thanks}\:\mathrm{for}\:\mathrm{checking} \\ $$$$\mathrm{I}\:\mathrm{corrected}\:\mathrm{it} \\ $$
