
Question Number 81615 by Zainal Arifin last updated on 14/Feb/20
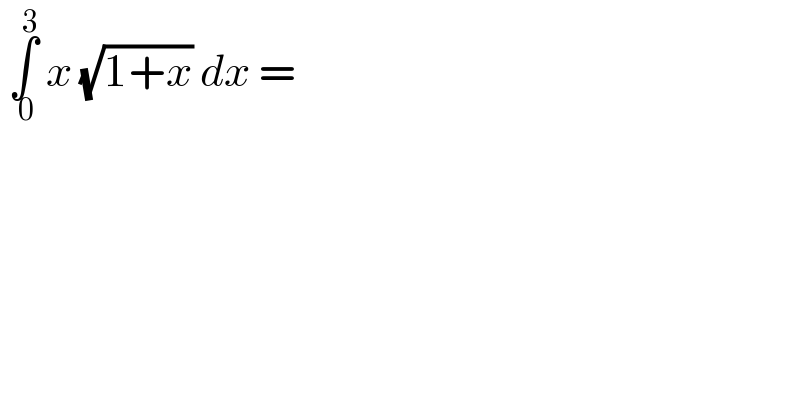
$$\:\underset{\:\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:{x}\:\sqrt{\mathrm{1}+{x}}\:{dx}\:= \\ $$
Answered by TANMAY PANACEA last updated on 14/Feb/20
![t^2 =1+x→2tdt=dx ∫_1 ^2 (t^2 −1)×t×2tdt ∫_1 ^2 2(t^4 −t^2 )dt 2×∣(t^5 /5)−(t^3 /3)∣_1 ^2 2×[(((32)/5)−(1/5))−((8/3)−(1/3))] 2×(((31)/5)−(7/3)) 2×(((93−35)/(15))) 2×((58)/(15))=((116)/(15))](Q81621.png)
$${t}^{\mathrm{2}} =\mathrm{1}+{x}\rightarrow\mathrm{2}{tdt}={dx} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)×{t}×\mathrm{2}{tdt} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{2}\left({t}^{\mathrm{4}} −{t}^{\mathrm{2}} \right){dt} \\ $$$$\mathrm{2}×\mid\frac{{t}^{\mathrm{5}} }{\mathrm{5}}−\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\mid_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\mathrm{2}×\left[\left(\frac{\mathrm{32}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{5}}\right)−\left(\frac{\mathrm{8}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\right)\right] \\ $$$$\mathrm{2}×\left(\frac{\mathrm{31}}{\mathrm{5}}−\frac{\mathrm{7}}{\mathrm{3}}\right) \\ $$$$\mathrm{2}×\left(\frac{\mathrm{93}−\mathrm{35}}{\mathrm{15}}\right) \\ $$$$\mathrm{2}×\frac{\mathrm{58}}{\mathrm{15}}=\frac{\mathrm{116}}{\mathrm{15}} \\ $$
Commented by zainal tanjung last updated on 14/Feb/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Commented by TANMAY PANACEA last updated on 14/Feb/20

$${most}\:{welcome} \\ $$
