
Question Number 133541 by bemath last updated on 22/Feb/21
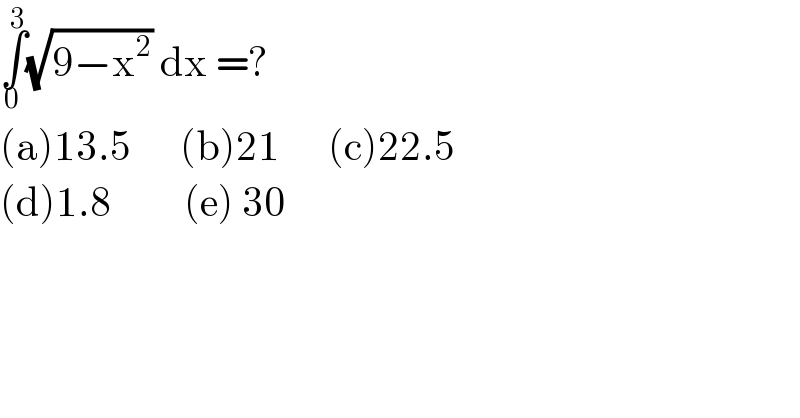
$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=? \\ $$$$\left(\mathrm{a}\right)\mathrm{13}.\mathrm{5}\:\:\:\:\:\:\left(\mathrm{b}\right)\mathrm{21}\:\:\:\:\:\:\left(\mathrm{c}\right)\mathrm{22}.\mathrm{5} \\ $$$$\left(\mathrm{d}\right)\mathrm{1}.\mathrm{8}\:\:\:\:\:\:\:\:\:\left(\mathrm{e}\right)\:\mathrm{30} \\ $$
Commented by MJS_new last updated on 23/Feb/21

$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{quarter}\:\mathrm{circle}\:\mathrm{of}\:\mathrm{radius}\:\mathrm{3}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{9}\pi}{\mathrm{4}}\approx\mathrm{7}.\mathrm{06858} \\ $$
Commented by bemath last updated on 23/Feb/21
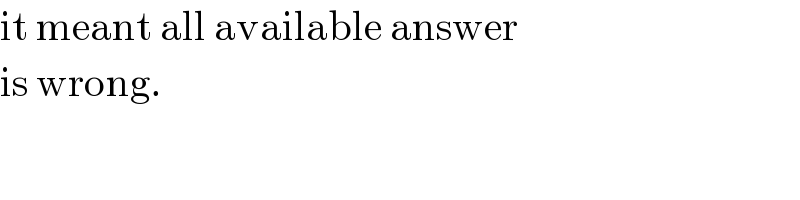
$$\mathrm{it}\:\mathrm{meant}\:\mathrm{all}\:\mathrm{available}\:\mathrm{answer} \\ $$$$\mathrm{is}\:\mathrm{wrong}.\: \\ $$
Answered by mathmax by abdo last updated on 23/Feb/21
![∫_0 ^3 (√(9−x^2 ))dx =_(x=3sint) 3∫_0 ^(π/2) cost(3cost)dt =9∫_0 ^(π/2) cos^2 t dt =(9/2)∫_0 ^(π/2) (1+cos(2t))dt =((9π)/4)+(9/4)[sin(2t)]_0 ^(π/2) =((9π)/4)](Q133732.png)
$$\int_{\mathrm{0}} ^{\mathrm{3}} \sqrt{\mathrm{9}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{x}=\mathrm{3sint}} \:\:\mathrm{3}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cost}\left(\mathrm{3cost}\right)\mathrm{dt}\:=\mathrm{9}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2}} \mathrm{t}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)\right)\mathrm{dt}\:=\frac{\mathrm{9}\pi}{\mathrm{4}}+\frac{\mathrm{9}}{\mathrm{4}}\left[\mathrm{sin}\left(\mathrm{2t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\mathrm{9}\pi}{\mathrm{4}} \\ $$
