
Question Number 155017 by SANOGO last updated on 24/Sep/21

$$\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{2}}} {E}\left({x}^{\mathrm{2}} \right){dx};\:{avec}\:{E}\left({x}\right)\:{la}\:{partie}\:{entiere} \\ $$
Answered by puissant last updated on 24/Sep/21
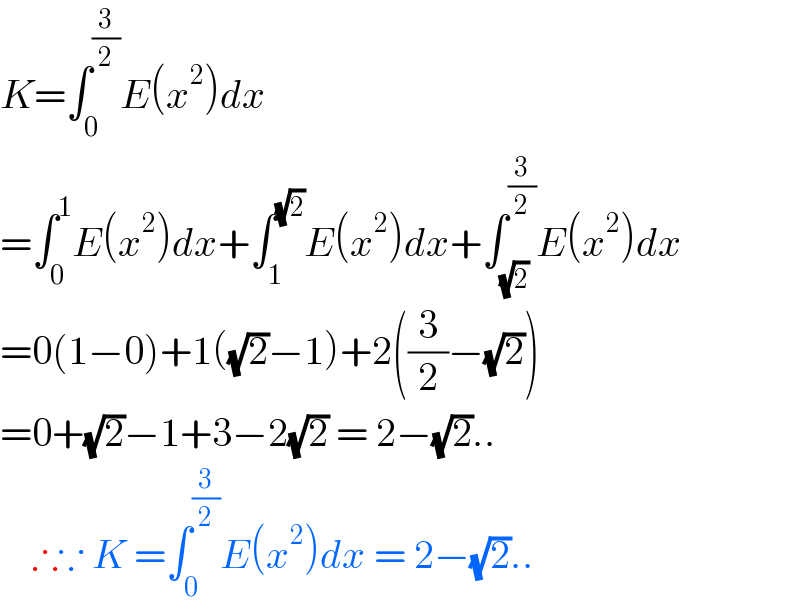
$${K}=\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{2}}} {E}\left({x}^{\mathrm{2}} \right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {E}\left({x}^{\mathrm{2}} \right){dx}+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} {E}\left({x}^{\mathrm{2}} \right){dx}+\int_{\sqrt{\mathrm{2}}} ^{\frac{\mathrm{3}}{\mathrm{2}}} {E}\left({x}^{\mathrm{2}} \right){dx} \\ $$$$=\mathrm{0}\left(\mathrm{1}−\mathrm{0}\right)+\mathrm{1}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)+\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{2}}−\sqrt{\mathrm{2}}\right) \\ $$$$=\mathrm{0}+\sqrt{\mathrm{2}}−\mathrm{1}+\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\:=\:\mathrm{2}−\sqrt{\mathrm{2}}.. \\ $$$$\:\:\:\:\therefore\because\:{K}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{3}}{\mathrm{2}}} {E}\left({x}^{\mathrm{2}} \right){dx}\:=\:\mathrm{2}−\sqrt{\mathrm{2}}.. \\ $$
Commented by SANOGO last updated on 24/Sep/21

$${merci}\:{bien}\:{courage} \\ $$
Commented by puissant last updated on 24/Sep/21
����������������
Commented by tabata last updated on 25/Sep/21

$${sir}\:{how}\:{you}\:{give}\:{the}\:{interval}\:{in}\:{this}\:{form} \\ $$$${can}\:{you}\:{give}\:{me}\:{the}\:{formulla}\:{of}\:{E}\left({x}\right)\:? \\ $$
