
Question Number 213518 by deleted31 last updated on 07/Nov/24
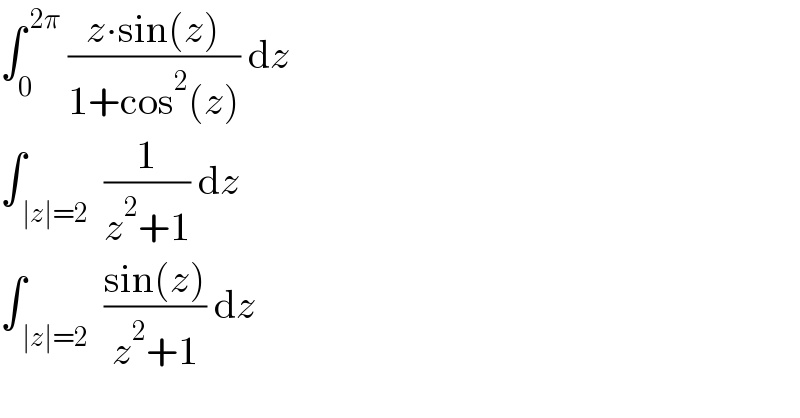
$$\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \:\frac{{z}\centerdot\mathrm{sin}\left({z}\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \left({z}\right)}\:\mathrm{d}{z} \\ $$$$\int_{\:\mid{z}\mid=\mathrm{2}} \:\frac{\mathrm{1}}{{z}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{d}{z} \\ $$$$\int_{\:\mid{z}\mid=\mathrm{2}} \:\frac{\mathrm{sin}\left({z}\right)}{{z}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{d}{z} \\ $$
Answered by Berbere last updated on 07/Nov/24
![∫_0 ^π ((zsin(z))/(1+cos^2 (z)))+∫_0 ^π ((sin(π+z)(π+z)dz)/(1+coz^2 (z))) =−π∫_0 ^π ((sin(z))/(1+cos^2 (z)))dz=πtan^(−1) (cos(z))]_0 ^π =−(π^2 /2) 2..=2iπ Res((1/(z^2 +1)),i;−i}=2iπ.((1/(2i))−(1/(2i)))=0 ..3 =∫((sin(z))/(1+z^2 ))dz=2iπ Res(((sin(z))/(1+z^2 )),z=i,−i) =2iπ[((sin(i))/(2i))+((sin(−i))/(−2i))) =2πsin(i)=−2πsh(1)](Q213531.png)
$$\int_{\mathrm{0}} ^{\pi} \frac{{zsin}\left({z}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left({z}\right)}+\int_{\mathrm{0}} ^{\pi} \frac{{sin}\left(\pi+\mathrm{z}\right)\left(\pi+{z}\right){dz}}{\mathrm{1}+{coz}^{\mathrm{2}} \left({z}\right)} \\ $$$$\left.=−\pi\int_{\mathrm{0}} ^{\pi} \frac{{sin}\left({z}\right)}{\mathrm{1}+{cos}^{\mathrm{2}} \left({z}\right)}{dz}=\pi\mathrm{tan}^{−\mathrm{1}} \left({cos}\left({z}\right)\right)\right]_{\mathrm{0}} ^{\pi} \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\mathrm{2}..=\mathrm{2}{i}\pi\:{Res}\left(\frac{\mathrm{1}}{{z}^{\mathrm{2}} +\mathrm{1}},{i};−{i}\right\}=\mathrm{2}{i}\pi.\left(\frac{\mathrm{1}}{\mathrm{2}{i}}−\frac{\mathrm{1}}{\mathrm{2}{i}}\right)=\mathrm{0} \\ $$$$..\mathrm{3} \\ $$$$=\int\frac{{sin}\left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}=\mathrm{2}{i}\pi\:{Res}\left(\frac{{sin}\left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} },{z}={i},−{i}\right) \\ $$$$=\mathrm{2}{i}\pi\left[\frac{{sin}\left({i}\right)}{\mathrm{2}{i}}+\frac{{sin}\left(−{i}\right)}{−\mathrm{2}{i}}\right) \\ $$$$=\mathrm{2}\pi{sin}\left({i}\right)=−\mathrm{2}\pi{sh}\left(\mathrm{1}\right) \\ $$$$ \\ $$
Commented by York12 last updated on 08/Nov/24
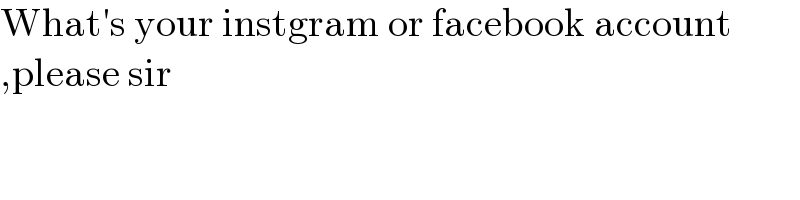
$$\mathrm{What}'\mathrm{s}\:\mathrm{your}\:\mathrm{instgram}\:\mathrm{or}\:\mathrm{facebook}\:\mathrm{account} \\ $$$$,\mathrm{please}\:\mathrm{sir} \\ $$
Commented by deleted31 last updated on 08/Nov/24

$$\mathrm{thx}... \\ $$
