
Question Number 12401 by sin (x) last updated on 21/Apr/17
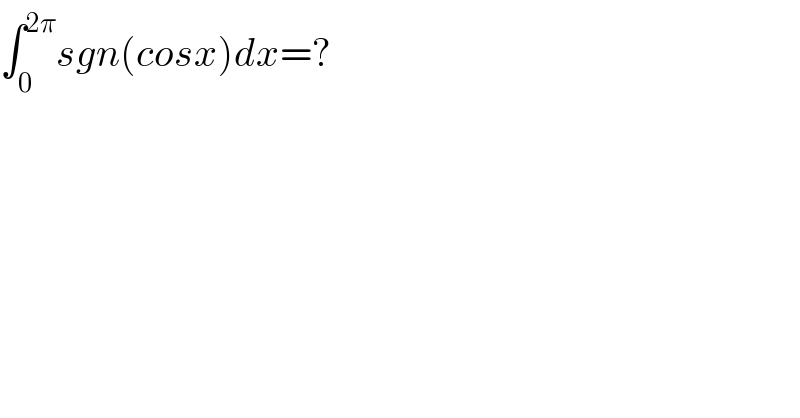
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sgn}\left({cosx}\right){dx}=? \\ $$
Commented by FilupS last updated on 21/Apr/17
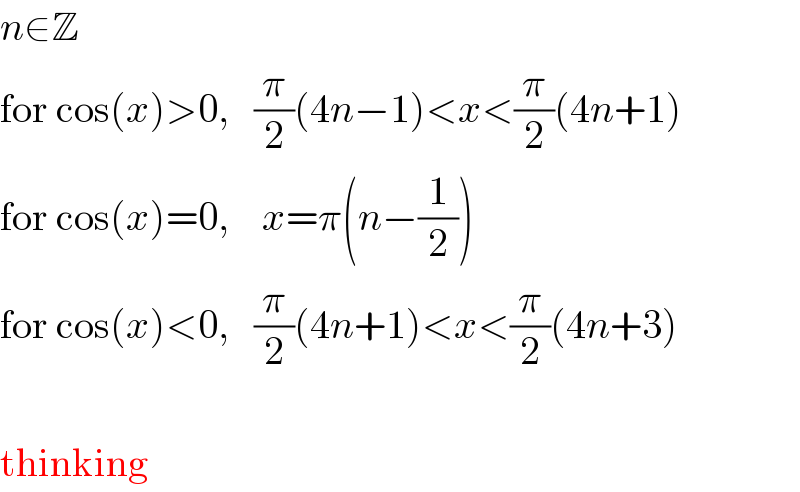
$${n}\in\mathbb{Z} \\ $$$$\mathrm{for}\:\mathrm{cos}\left({x}\right)>\mathrm{0},\:\:\:\frac{\pi}{\mathrm{2}}\left(\mathrm{4}{n}−\mathrm{1}\right)<{x}<\frac{\pi}{\mathrm{2}}\left(\mathrm{4}{n}+\mathrm{1}\right) \\ $$$$\mathrm{for}\:\mathrm{cos}\left({x}\right)=\mathrm{0},\:\:\:\:{x}=\pi\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{for}\:\mathrm{cos}\left({x}\right)<\mathrm{0},\:\:\:\frac{\pi}{\mathrm{2}}\left(\mathrm{4}{n}+\mathrm{1}\right)<{x}<\frac{\pi}{\mathrm{2}}\left(\mathrm{4}{n}+\mathrm{3}\right) \\ $$$$\: \\ $$$$\mathrm{thinking} \\ $$
Answered by mrW1 last updated on 21/Apr/17
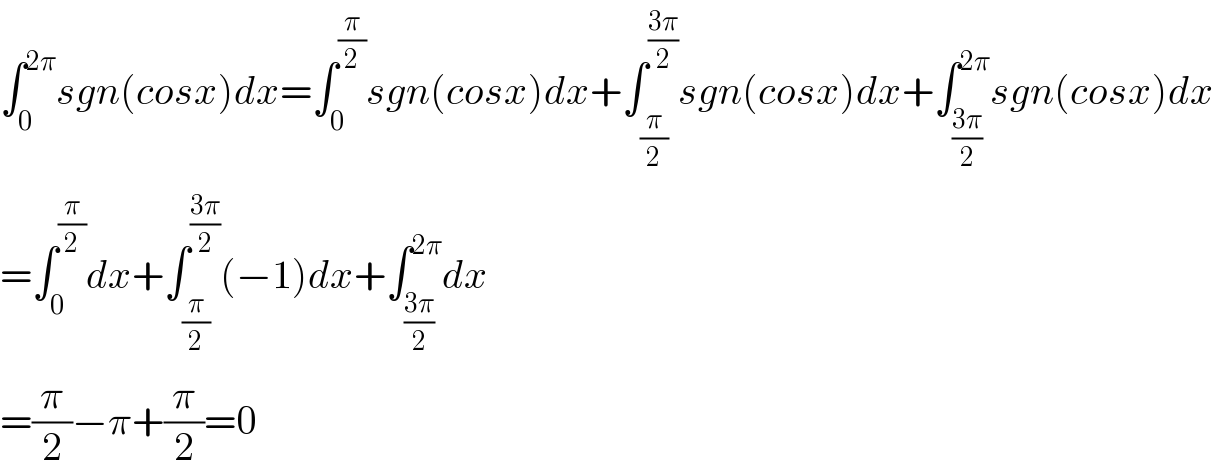
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sgn}\left({cosx}\right){dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sgn}\left({cosx}\right){dx}+\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} {sgn}\left({cosx}\right){dx}+\int_{\frac{\mathrm{3}\pi}{\mathrm{2}}} ^{\mathrm{2}\pi} {sgn}\left({cosx}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}+\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\mathrm{3}\pi}{\mathrm{2}}} \left(−\mathrm{1}\right){dx}+\int_{\frac{\mathrm{3}\pi}{\mathrm{2}}} ^{\mathrm{2}\pi} {dx} \\ $$$$=\frac{\pi}{\mathrm{2}}−\pi+\frac{\pi}{\mathrm{2}}=\mathrm{0} \\ $$
Commented by FilupS last updated on 22/Apr/17

$$\mathrm{ah}!\:\mathrm{simple} \\ $$
